Question

请考生在第（1），（2），（3）题中任选一题作答，如果多做，则按所做的第一题记分．
（1）选修4-1：几何证明选讲
如图，在△ABC中，D是AC的中点，E是BD的中点，AE的延长线交BC于F．
（Ⅰ）求

BF

FC

的值；
（Ⅱ）若△BEF的面积为S₁，四边形CDEF的面积为S₂，求S₁：S₂的值．
（2）选修4-4：坐标系与参数方程
以直角坐标系的原点O为极点，a=

π

6

轴的正半轴为极轴，且两个坐标系取相等的单位长度．已知直线l经过点P（1，1），倾斜角a=

π

6

．
（ I）写出直线l的参数方程；
（ II）设l与圆ρ=2相交于两点A、B，求点P到A、B两点的距离之积．
（3）选修4-5：不等式选讲
已知函数f（x）=|2x+1|+|2x-3|．
（I）求不等式f（x）≤6的解集；
（II）若关于x的不等式f（x）＞a恒成立，求实数a的取值范围．

Answer 1

分析：（1）：（Ⅰ）过D点作DG∥BC，并交AF于G点，再利用△BEF≌△DEG，则BF=DG，得出比例关系：BF：FC=DG：FC，从而得出BF：FC=1：2；
（Ⅱ）先由（1）知BF：BC=1：3，又由BE：BD=1：2可知h₁：h₂=1：2，其中h₁、h₂分别为△BEF和△BDC的高，由此求得面积比．
（2）：（I）根据直线经过的点的坐标及直线的倾斜角，求出直线的参数方程．
（II） 设A，B对应的参数为t₁和t₂，以直线l的参数方程代入圆的方程整理得到 t²+（

3

+1）t-2=0，由|PA|•|PB|=|t₁t₂|求出点P到A、B两点的距离之积．
（3）：（I）首先要去掉绝对值，因此要进行分类讨论：①x＞

3

2

；②-

1

2

≤x≤

3

2

；③x＜-

1

2

，然后再解一元一次不等式进行求解；
（II）对绝对值不等式进行放缩，可得|2x+1|+|2x-3|≥|（2x+1）-（2x-3）|=4，从而求出a的范围．

解答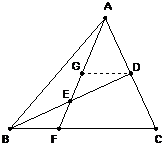：证明：（1）、（Ⅰ）过D点作DG∥BC，并交AF于G点，
∵E是BD的中点，∴BE=DE，
      又∵∠EBF=∠EDG，∠BEF=∠DEG，
∴△BEF≌△DEG，则BF=DG，
∴BF：FC=DG：FC，
又∵D是AC的中点，则DG：FC=1：2，
则BF：FC=1：2；
即

BF

FC

=

1

2

（Ⅱ）若△BEF以BF为底，△BDC以BC为底，
则由（1）知BF：BC=1：3，
又由BE：BD=1：2可知h₁：h₂=1：2，其中h₁、h₂分别为△BEF和△BDC的高，
则

S△BEF

S△BDC

=

1

3

×

1

2

=

1

6

，则S₁：S₂=1：5
（2）、（I）直线的参数方程是

x=1+ 3 2 t y=1+ 1 2 t

（t是参数）．
（II）因为点A，B都在直线l上，所以可设它们对应的参数为t1和t2，
圆化为直角坐标系的方程   x²+y²=4，
以直线l的参数方程代入圆的方程整理得到 t²+（

3

+1）t-2=0  ①，
因为t₁和t₂是方程①的解，从而 t₁t₂=-2．
∴|PA|•|PB|=|t₁t₂|=|-2|=2．
（3）（I）原不等式等价于

x＞ 3 2 (2x+1)+(2x-3)≤6

或

- 1 2 ≤x≤ 3 2 (2x+1)-(2x-3)≤6

或

x＜- 1 2 -(2x+1)-(2x-3)≤6

解得

3

2

＜x≤2或-

1

2

≤x≤

3

2

或-1≤x＜-

1

2

，
即不等式的解集为{x|-1≤x≤2}
（II）∵|2x+1|+|2x-3|≥|（2x+1）-（2x-3）|=4，
∴a＜4．

点评：本题C题考查绝对值不等式的几何意义，是基础题；B题：考查的知识点是相交弦定理及相似三角形的性质，其中根据相交弦定理及三角形相似的性质，得到比例式，是解答本题的关键；A题考查把极坐标方程和参数方程化为普通方程的方法，点到直线的距离公式的应用，将参数方程化为普通方程是解答关键．