摘要：∴h＝为所求.评述:本题重点考查棱柱.直线与平面所成的角.二面角等概念.能力方面主要考查逻辑思维能力.空间想象能力.运算能力.本题(Ⅲ)的解法二用体积法求出点到面的距离.其优点是不会由于证明过程中叙述不当而被扣分.只要计算准确.就可以得到满分,另外较之方法一思维也要简单.在解法一中要判断出BH∥A1E,∠DEA1＝∠CBH.这需要较好的空间想象能力和逻辑推理能力.由此可见.一些数学问题的一些特殊解法往往使思维.推导.运算得以大大简化.
网址：http://m.1010jiajiao.com/timu_id_425248[举报]
如图(1)所示，在正三棱柱ABC—A1B1C 1中，AB=3，AA1=4，M为AA1的中点，P是BC上一点，且由P沿棱柱侧面经过棱CC1到M的最短路线长为
，设这条最短路线与CC1的交点为N.求：
，设这条最短路线与CC1的交点为N.求： 
(1)
(1)该三棱柱的侧面展开图的对角线长；
(2)PC和NC的长；
(3)平面NMP与平面ABC所成二面角(锐角)的大小(用反三角函数表示).
查看习题详情和答案>>如图，在正三棱柱ABC-A1B1C1中，AB=3，AA1=4,M为AA1的中点，P是BC上一点，且由P沿棱柱侧面经过棱CC1到M点的最短路线长为
，设这条最短路线与C1C的交点为N.求
（1）该三棱柱的侧面展开图的对角线长；
（2）PC和NC的长；
（3）平面NMP和平面ABC所成二面角（锐角）的正切值.
16.如图，在正三棱柱ABC—A1B1C1中，AB=3,AA1=4.M为AA1的中点，P是BC上一点，且由P沿棱柱侧面经过棱CC1到M的最短路线长为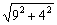
,设这条最短路线与CC1的交点为N.求：
,设这条最短路线与CC1的交点为N.求： 
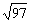
（Ⅰ）该三棱柱的侧面展开图的对角线长；
（Ⅱ）PC和NC的长；
（Ⅲ）平面NMP与平面ABC所成二面角（锐角）的大小（用反三角函数表示）.
查看习题详情和答案>>
（本小题满分13分）已知正四棱锥P—ABCD的高为
，底面边长为
，其内接正四棱柱EFGH—E1F1G1H1的四个顶点E、F、G、H在底面上，另外四个顶点E1、F1、G1、H1分别在棱PA、PB、PC、PD上（如图所示），设正四棱柱的底面边长为
．
，求出函数
的解析式；
在正三棱柱
中，AB＝2，
，由顶点B沿棱柱侧面经过棱
到顶点
的最短路线与
的值;
与平面ABC所成二面角（锐角）的大小