题目内容
16.如图,在正三棱柱ABC—A1B1C1中,AB=3,AA1=4.M为AA1的中点,P是BC上一点,且由P沿棱柱侧面经过棱CC1到M的最短路线长为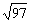
(Ⅰ)该三棱柱的侧面展开图的对角线长;
(Ⅱ)PC和NC的长;
(Ⅲ)平面NMP与平面ABC所成二面角(锐角)的大小(用反三角函数表示).
16.主要考查直线与平面的位置关系、棱柱等基本知识,考查空间想象能力、逻辑思维能力和运算能力.
解:
(Ⅰ)正三棱柱ABC—A1B1C1的侧面展开图是一个长为9,宽为4的矩形,其对角线长为![]() =
=![]() .
.
(Ⅱ)如图1,将侧面BB1C1C绕棱CC1旋转120°使其与侧面AA1C1C在同一平面上,点P运动到点P1的位置,连接MP1,则MP1就是由点P沿棱柱侧面经过棱CC1到点M的最短路线.
设PC=x,则P1C=x.在Rt△MAP1中,
由勾股定理得(3+x)2+22=29,
求得x=2.
∴PC=P1C=2.∵![]() =
=![]() =
=![]() ,∴NC=
,∴NC=![]() .
.
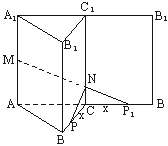
图1
(Ⅲ)如图2,连接PP1,则PP1就是平面NMP与平面ABC的交线.作NH⊥PP1于H,又CC1⊥平面ABC,连结CH,由三垂线定理得CH⊥PP1.
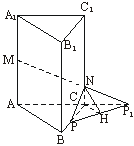
图2
∴∠NHC就是平面NMP与平面ABC所成二面角的平面角(锐角).
在Rt△PHC中,∵∠PCH=![]() ∠PCP1=60°,
∠PCP1=60°,
∴CH=![]() =1.在Rt△NCH中,tanNHC=
=1.在Rt△NCH中,tanNHC=![]() =
=![]() =
=![]() ,
,
故平面NMP与平面ABC所成二面角(锐角)的大小为arctan![]() .
.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )
如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
 如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2.
如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2. 如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,
如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上, (2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.
(2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.