题目内容
如图(1)所示,在正三棱柱ABC—A1B
(1)
(1)该三棱柱的侧面展开图的对角线长;
(2)PC和NC的长;
(3)平面NMP与平面ABC所成二面角(锐角)的大小(用反三角函数表示).
解析:(1)正三棱柱ABC—A1B![]() .
.
(2)如图(2)所示,将侧面BB

(2)
设PC=x,则P
在Rt△MAP1中,由勾股定理得(3+x)2+22=29,求得x=2.
∴PC=P
∵![]() ,
,
∴NC=![]() .
.
(3)如图(3)所示,连结PP1.
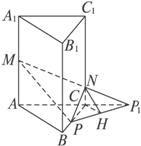
(3)
则PP1就是平面NMP与平面ABC的交线.
作NH⊥PP1于H,又CC1⊥平面ABC,连结CH.
由三垂线定理得CH⊥PP1,
∴∠NHC就是平面NMP与平面ABC所成二面角的平面角(锐角).
在Rt△PHC中,
∵∠PCH=![]() ∠PCP1=60°,
∠PCP1=60°,
∴CH=![]() =1.
=1.
在Rt△NCH中,
tan∠NHC=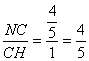 .
.
故平面NMP与平面ABC所成二面角(锐角)的大小为arctan![]() .
.

练习册系列答案
相关题目