摘要：∴tanDFA＝即所求二面角的正切值.评述:欲求二面角的大小应遵循“构造―证明―计算 的步骤行事.这里首要的一步且先“出现两个面的交线(棱) 否则构造难以实行.
网址：http://m.1010jiajiao.com/timu_id_425192[举报]
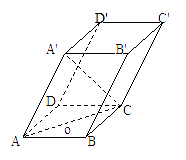如图，平行六面体ABCD－A'B'C'D'中，AC＝2
，BC＝AA'＝A'C＝2，∠ABC＝90°，点O是点A'在底面ABCD上的射影，且点O恰好落在AC上.
（1）求侧棱AA'与底面ABCD所成角的大小；
（2）求侧面A'ADD'底面ABCD所成二面角的正切值；
（3）求四棱锥C－A'ADD'的体积.
查看习题详情和答案>>
如图，在四棱锥S-ABCD中，SA=AB=2，SB=SD=2| 2 |
（I）证明：CD⊥平面SAE；
（II）求侧面SBC和底面ABCD所成二面角的正切值．
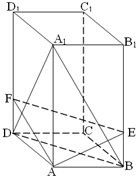正四棱柱ABCD-A1B1C1D1的底面边长是| 3 |
（1）求证：A1C⊥面AEF；
（2）求截面AEF与底面ABCD所成二面角θ的正切值．
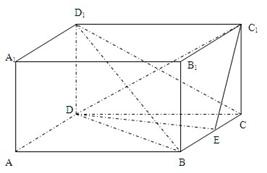如图，ABCD-A1B1C1D1是正四棱柱，侧棱长为 1，底面边长为 2，E是棱BC的中点．
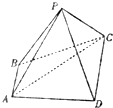（2012•安徽模拟）如图，已知四棱锥P-ABCD的底面ABCD是直角梯形，AB∥CD，∠BAD=90°，PB=PC=CD=2AB=4，AC=2