题目内容
 如图,在四棱锥S-ABCD中,SA=AB=2,SB=SD=2
如图,在四棱锥S-ABCD中,SA=AB=2,SB=SD=2| 2 |
(I)证明:CD⊥平面SAE;
(II)求侧面SBC和底面ABCD所成二面角的正切值.
分析:(I)连接AC,结合已知条件,可在菱形ABCD中证出CD⊥AE.再在△SAB、△SAD中利用勾股定理的逆定理,证出SA⊥AB和
SA⊥AD,结合线面垂直的判定定理得到SA⊥平面ABCD,从而SA⊥CD.最后结合CD⊥AE,AE、SA是平面SAE内的相交直线,可得CD⊥平面SAE;
(II)取BC的中点F,连接AF、SF,可证出AF⊥BC且SF⊥BC,所以∠SFA为二面角S-BC-A的平面角.最后在Rt△ASF中,利用正切的定义得到tan∠SFA=
=
,即得侧面SBC和底面ABCD所成二面角的正切值.
SA⊥AD,结合线面垂直的判定定理得到SA⊥平面ABCD,从而SA⊥CD.最后结合CD⊥AE,AE、SA是平面SAE内的相交直线,可得CD⊥平面SAE;
(II)取BC的中点F,连接AF、SF,可证出AF⊥BC且SF⊥BC,所以∠SFA为二面角S-BC-A的平面角.最后在Rt△ASF中,利用正切的定义得到tan∠SFA=
| SA |
| AF |
2
| ||
| 3 |
解答:解:(I)如图,连接AC
∵在菱形ABCD中,∠ADC=60°,E是线段CD的中点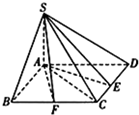
∴CD⊥AE
又∵SA=AB=2,SB=2
∴SA2+AB2=8=SB2,可得SA⊥AB.同理得到SA⊥AD
∵AB、AD是平面ABCD内的相交直线
∴SA⊥平面ABCD
又∵CD?平面ABCD,∴SA⊥CD
∵CD⊥AE,AE、SA是平面SAE内的相交直线
∴CD⊥平面SAE
(II)取BC的中点F,连接AF、SF
由(I)的证明过程,类似地可得AF⊥BC且SF⊥BC
∴∠SFA为二面角S-BC-A的平面角
∵Rt△ASF中,AF=
,SA=2
∴tan∠SFA=
=
即侧面SBC和底面ABCD所成二面角的正切值为
.
∵在菱形ABCD中,∠ADC=60°,E是线段CD的中点

∴CD⊥AE
又∵SA=AB=2,SB=2
| 2 |
∴SA2+AB2=8=SB2,可得SA⊥AB.同理得到SA⊥AD
∵AB、AD是平面ABCD内的相交直线
∴SA⊥平面ABCD
又∵CD?平面ABCD,∴SA⊥CD
∵CD⊥AE,AE、SA是平面SAE内的相交直线
∴CD⊥平面SAE
(II)取BC的中点F,连接AF、SF
由(I)的证明过程,类似地可得AF⊥BC且SF⊥BC
∴∠SFA为二面角S-BC-A的平面角
∵Rt△ASF中,AF=
| 3 |
∴tan∠SFA=
| SA |
| AF |
2
| ||
| 3 |
即侧面SBC和底面ABCD所成二面角的正切值为
2
| ||
| 3 |
点评:本题给出底面为菱形、一条侧棱垂直于底的四棱锥,要我们证明线面垂直并求二面角的正切值,着重考查了线面垂直的判定与性质和平面与平面所成角等知识点,属于中档题.

练习册系列答案
相关题目
 如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE=
如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE= 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点 如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=
如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD= 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点. 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,