Question

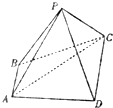（2012•安徽模拟）如图，已知四棱锥P-ABCD的底面ABCD是直角梯形，AB∥CD，∠BAD=90°，PB=PC=CD=2AB=4，AC=2

7

，平面 BPC丄平面 ABCD
（1）求四棱锥P-ABCD的体积；
（2）求平面PAD与平面FBC所成二面角的正切值．

Answer 1

分析：（1）取BC的中点O，连接PO，证明PO⊥平面ABCD，计算梯形ABCD的面积，即可求得四棱锥P-ABCD的体积；
（2）利用平面 BPC丄平面ABCD，证明OD⊥平面 BPC，延长CB与DA交于E，连接PE，过O作ON⊥PE，连DN，则∠DNO为所求二面角的平面角，故可求．

解答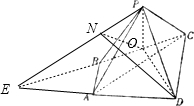：解：（1）在直角梯形ABCD中，由AC=2

7

，CD=2AB=4，∠ADC=90°，可得AD=2

3

，BC=BD=4
∴△BPC为等边三角形
取BC的中点O，连接PO，则PO⊥BC
∵平面 BPC丄平面ABCD，平面 BPC∩平面ABCD=BC
∴PO⊥平面ABCD
∴四棱锥P-ABCD的体积为

1

3

×SABCD×PO=

1

3

×

1

2

×(2+4)×2

3

×2

3

=12；
（2）连接OD，由（1）可得△BDC为等边三角形，而O为BC的中点，∴OD⊥BC
∵平面 BPC丄平面ABCD，平面 BPC∩平面ABCD=BC，∴OD⊥平面 BPC
延长CB与DA交于E，连接PE，过O作ON⊥PE，连DN，则∠DNO为所求二面角的平面角
∵ON=

3

4

PC=3，OD=2

3

，∴tan∠DNO=

OD

ON

=

2 3

3

．

点评：本题考查四棱锥的体积，考查面面角，解题的关键是确定四棱锥的高，确定面面角．