题目内容
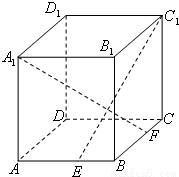
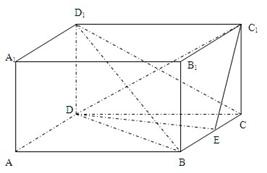 如图,ABCD-A1B1C1D1是正四棱柱,侧棱长为 1,底面边长为 2,E是棱BC的中点.
如图,ABCD-A1B1C1D1是正四棱柱,侧棱长为 1,底面边长为 2,E是棱BC的中点.(1)求三棱锥D1-DBC的体积;
(2)证明 BD1∥平面C1DE;
(3)求面C1DE与面CDE所成二面角的正切值.
分析:(1)分别求出高DD1和底面面积S△BCD,最后由三棱锥的体积公式求其体积.
(2)根据线面平行的判定理,只要证明EF∥BD1即可.
(3)先过C作CG⊥DE交DE于G,连接则DE⊥C1G作出二面角的平面角来,然后在Rt△CDE中,CD=2,CE=1,DE=
,求得CG=
,再由CC1=1,通过tan∠C1GC=
求解.
(2)根据线面平行的判定理,只要证明EF∥BD1即可.
(3)先过C作CG⊥DE交DE于G,连接则DE⊥C1G作出二面角的平面角来,然后在Rt△CDE中,CD=2,CE=1,DE=
| 5 |
| 2 | ||
|
| |C1C| |
| |CG| |
解答:解:(1)∵BC=CD=2∴=
×2×2=2
又∵DD1=1
∴三棱锥D1-DBC的体积=
S△BCDDD1=
×2×1=
(2分)
(2)设C1D∩CD1=F
连接EF∵E为BC的中点F为CD1的中点
∴EF是△BCD1的中位线∴EF∥BD1(3分)
又BD1在平面C1DE外,EF在平面C1DE内
∴BD1∥平面C1DE(4分)
(3)过C作CG⊥DE交DE于G,连接
则DE⊥C1G∴∠C1GC是二面角C1-DE-C的一个平面角(5分)
在Rt△CDE中,CD=2,CE=1,DE=
∴CG=
又∵CC1=1△CC1G是直角三角形(6分)
∴tan∠C1GC=
=
=
(7分)
| 1 |
| 2 |
又∵DD1=1
∴三棱锥D1-DBC的体积=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
(2)设C1D∩CD1=F
连接EF∵E为BC的中点F为CD1的中点
∴EF是△BCD1的中位线∴EF∥BD1(3分)
又BD1在平面C1DE外,EF在平面C1DE内
∴BD1∥平面C1DE(4分)
(3)过C作CG⊥DE交DE于G,连接
则DE⊥C1G∴∠C1GC是二面角C1-DE-C的一个平面角(5分)
在Rt△CDE中,CD=2,CE=1,DE=
| 5 |
∴CG=
| 2 | ||
|
∴tan∠C1GC=
| |C1C| |
| |CG| |
| 1 | ||||
|
| ||
| 2 |
点评:本题主要考查线面平行的判定定理,三棱锥的体积公式及二面角的几何求法,一般来讲,是一作,二找,三证.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
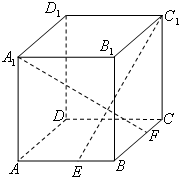 如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.
如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF. 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是