题目内容
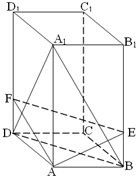 正四棱柱ABCD-A1B1C1D1的底面边长是
正四棱柱ABCD-A1B1C1D1的底面边长是| 3 |
(1)求证:A1C⊥面AEF;
(2)求截面AEF与底面ABCD所成二面角θ的正切值.
分析:(1)连接A1C,证明AE⊥A1C,AF⊥A1C,利用直线与平面垂直的判定定理证明A1C⊥面AEF;
(2)如图说明∠NAO=θ就是截面AEF与底面ABCD所成二面角θ,通过解三角形,求出AC,BE,即可求解θ的正切值.
(2)如图说明∠NAO=θ就是截面AEF与底面ABCD所成二面角θ,通过解三角形,求出AC,BE,即可求解θ的正切值.
解答: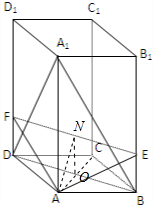 证明:(1)连接A1C
证明:(1)连接A1C
正四棱柱⇒CB⊥平面ABB1A1⇒CB⊥AE
又∵AE⊥A1B
∴AE⊥平面A1BC⇒AE⊥A1C
同理可得:AF⊥A1C
∴A1C⊥平面AEF
(2)∵AE⊥A1B⇒Rt△ABA1∽Rt△ABE⇒∠ABA1=∠BEA,
如图EF的中点为N,AC 的中点为O,连结NO,则∠NAO=θ,
又 底面边长是
,侧棱长是3
∴tan∠ABA1=
,∠ABA1=
得 ∠EAB=
,BE=1
同理 DF=1
又 AC=
,
∴tanθ=
=
=
.
 证明:(1)连接A1C
证明:(1)连接A1C正四棱柱⇒CB⊥平面ABB1A1⇒CB⊥AE
又∵AE⊥A1B
∴AE⊥平面A1BC⇒AE⊥A1C
同理可得:AF⊥A1C
∴A1C⊥平面AEF
(2)∵AE⊥A1B⇒Rt△ABA1∽Rt△ABE⇒∠ABA1=∠BEA,
如图EF的中点为N,AC 的中点为O,连结NO,则∠NAO=θ,
又 底面边长是
| 3 |
∴tan∠ABA1=
| 3 |
| π |
| 3 |
得 ∠EAB=
| π |
| 6 |
同理 DF=1
又 AC=
| 6 |
∴tanθ=
| BE | ||
|
| 2 | ||
|
| ||
| 3 |
点评:本题考查直线与平面垂直的判定定理,二面角的求法,考查空间想象能力与计算能力.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
顶点在同一球面上的正四棱柱ABCD-A′B′C′D′中,AB=1,AA′=
,则A、C两点间的球面距离为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=
如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=| 3 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
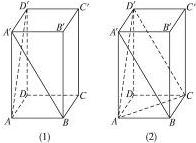 如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是
如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是