摘要:如图9―13.∠BAD=90°的等腰直角三角形ABD与正三角形CBD所在平面互相垂直.E是BC的中点.则AE与平面BCD所成角的大小为 .
网址:http://m.1010jiajiao.com/timu_id_424835[举报]
(04年上海卷文)(本题满分14分) 第1小题满分6分, 第2小题满分8分
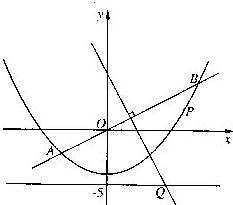
如图, 直线y=![]() x与抛物线y=
x与抛物线y=![]() x2-4交于A、B两点, 线段AB的垂直平分线与直线y=-5交于Q点.
x2-4交于A、B两点, 线段AB的垂直平分线与直线y=-5交于Q点.
(1) 求点Q的坐标;
(2) 当P为抛物线上位于线段AB下方
(含A、B) 的动点时, 求ΔOPQ面积的最大值.
查看习题详情和答案>>
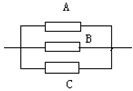 如图,A,B,C表示3种开关,设在某段时间内它们正常工作的概率是分别是0.9,0.8,0.7,如果系统中至少有1个开关能正常工作,那么该系统正常工作的概率是( )
如图,A,B,C表示3种开关,设在某段时间内它们正常工作的概率是分别是0.9,0.8,0.7,如果系统中至少有1个开关能正常工作,那么该系统正常工作的概率是( )| A、0.504 | B、0.496 | C、0.994 | D、0.06 |
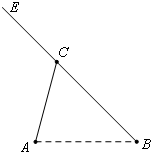 如图,A,B,C是三个汽车站,AC,BE是直线型公路.已知AB=120km,∠BAC=75°,∠ABC=45°.有一辆车(称甲车)以每小时96(km)的速度往返于车站A,C之间,到达车站后停留10分钟;另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E,途经车站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.
如图,A,B,C是三个汽车站,AC,BE是直线型公路.已知AB=120km,∠BAC=75°,∠ABC=45°.有一辆车(称甲车)以每小时96(km)的速度往返于车站A,C之间,到达车站后停留10分钟;另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E,途经车站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.(1)计算A,C两站距离,及B,C两站距离;
(2)若甲、乙两车上各有一名旅客需要交换到对方汽车上,问能否在车站C处利用停留时间交换.
(3)求10点时甲、乙两车的距离.
(参考数据:
| 2 |
| 3 |
| 6 |
| 331 |
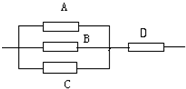 如图,A,B,C,D表示4种开关,设在某段时间内它们能通电的概率是分别是0.9,0.8,0.7,0.8,那么该系统能通电的概率是
如图,A,B,C,D表示4种开关,设在某段时间内它们能通电的概率是分别是0.9,0.8,0.7,0.8,那么该系统能通电的概率是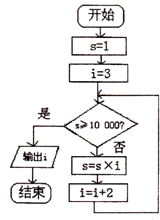 (2010•上海模拟)如果执行如图的程序框图,那么输出的i=
(2010•上海模拟)如果执行如图的程序框图,那么输出的i=