题目内容
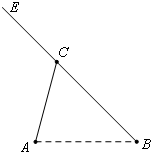 如图,A,B,C是三个汽车站,AC,BE是直线型公路.已知AB=120km,∠BAC=75°,∠ABC=45°.有一辆车(称甲车)以每小时96(km)的速度往返于车站A,C之间,到达车站后停留10分钟;另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E,途经车站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.
如图,A,B,C是三个汽车站,AC,BE是直线型公路.已知AB=120km,∠BAC=75°,∠ABC=45°.有一辆车(称甲车)以每小时96(km)的速度往返于车站A,C之间,到达车站后停留10分钟;另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E,途经车站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.(1)计算A,C两站距离,及B,C两站距离;
(2)若甲、乙两车上各有一名旅客需要交换到对方汽车上,问能否在车站C处利用停留时间交换.
(3)求10点时甲、乙两车的距离.
(参考数据:
| 2 |
| 3 |
| 6 |
| 331 |
分析:(1)在△ABC中,∠ACB=60°,利用
=
=
,可求A、C,B、C两站距离;
(2)先分别求甲车从车站A开到车站C,乙车从车站B开到车站C的时间,从而可确定两名旅客能否在车站C处利用停留时间交换;
(3)先求10点时甲车离开C站的距离为,乙车离开C站的距离,再利用余弦定理求两车的距离.
| AB |
| sin60° |
| BC |
| sin75° |
| AC |
| sin45° |
(2)先分别求甲车从车站A开到车站C,乙车从车站B开到车站C的时间,从而可确定两名旅客能否在车站C处利用停留时间交换;
(3)先求10点时甲车离开C站的距离为,乙车离开C站的距离,再利用余弦定理求两车的距离.
解答:解:(1)在△ABC中,∠ACB=60°.∵
=
=
,
∴AC=
=
=40
≈96(km),BC=
=
=60
+20
≈132(km).
(2)甲车从车站A开到车站C约用时间为
=1(小时)=60(分钟),即9点到C站,至9点零10分开出.
乙车从车站B开到车站C约用时间为
=1.1(小时)=66(分钟),即9点零6分到站,9点零16分开出.
则两名旅客可在9点零6分到10分这段时间内交换到对方汽车上.
(3)10点时甲车离开C站的距离为
×96=80(km),乙车离开C站的距离为
×120=88(km),
两车的距离等于
=8
=8
≈8×18.2=145.6(km)
| AB |
| sin60° |
| BC |
| sin75° |
| AC |
| sin45° |
∴AC=
| 120sin45° |
| sin60° |
120×
| ||||
|
| 6 |
| 120sin75° |
| sin60° |
120×
| ||||||
|
| 2 |
| 6 |
(2)甲车从车站A开到车站C约用时间为
| 96 |
| 96 |
乙车从车站B开到车站C约用时间为
| 132 |
| 120 |
则两名旅客可在9点零6分到10分这段时间内交换到对方汽车上.
(3)10点时甲车离开C站的距离为
| 50 |
| 60 |
| 44 |
| 60 |
两车的距离等于
| 802+882-2×80×88×cos120° |
| 100+121+110 |
| 331 |
点评:本题主要考查利用正弦、余弦定理解决实际问题,关键是构建三角形,确定边角关系.

练习册系列答案
相关题目
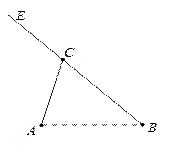
 站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.
站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出. ,
, ,
, ,
, )
)

 ,
, ,
, ,
, )
)
 ,
, ,
, ,
, )
)