题目内容
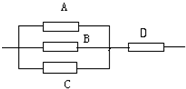 如图,A,B,C,D表示4种开关,设在某段时间内它们能通电的概率是分别是0.9,0.8,0.7,0.8,那么该系统能通电的概率是
如图,A,B,C,D表示4种开关,设在某段时间内它们能通电的概率是分别是0.9,0.8,0.7,0.8,那么该系统能通电的概率是0.7952
0.7952
.分析:记“A、B、C三个开关至少有一个正常”为事件E,“D正常”为事件F,“系统能通电”为事件D;由电路知识,可得电路通电,必须是E与F两个条件同时满足;由对立事件的概率性质可得P(E),而已知P(F),由相互独立事件的概率公式,计算可得答案.
解答:解:根据题意,电路通电,必须是“A、B、C三个开关至少有一个正常”与“D正常”两个条件同时满足;
记“A、B、C三个开关至少有一个正常”为事件E,“D正常”为事件F,“系统能通电”为事件D;
易得P(E)=1-P(
)=1-0.1×0.2×0.3=0.994,
P(F)=0.8;
P(D)=0.8×0.994=0.7952;
故答案为0.7952.
记“A、B、C三个开关至少有一个正常”为事件E,“D正常”为事件F,“系统能通电”为事件D;
易得P(E)=1-P(
. |
| A |
. |
| B |
. |
| C |
P(F)=0.8;
P(D)=0.8×0.994=0.7952;
故答案为0.7952.
点评:本题考查相互独立事件的概率计算以及对立事件的概率性质,求P(E)时,可以结合“互为对立事件的两个事件的概率之和为1”这一性质解题,可以避免分类讨论,简化解题过程.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 12、如图,A,B,C,D四点都在平面a,b外,它们在a内的射影A1,B1,C1,D1是平行四边形的四个顶点,在b内的射影A2,B2,C2,D2在一条直线上,求证:ABCD是平行四边形.
12、如图,A,B,C,D四点都在平面a,b外,它们在a内的射影A1,B1,C1,D1是平行四边形的四个顶点,在b内的射影A2,B2,C2,D2在一条直线上,求证:ABCD是平行四边形. 如图,A,B,C,D为空间四点,在△ABC中,
如图,A,B,C,D为空间四点,在△ABC中, 如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC=
如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC= 如图,A、B、C、D是某煤矿的四个采煤点,l是公路,图中所标线段为道路,ABQP、BCRQ、CDSR近似于正方形.已知A、B、C、D四个采煤点每天的采煤量之比约为5:1:2:3,运煤的费用与运煤的路程、所运煤的重量都成正比.现要从P、Q、R、S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在( )
如图,A、B、C、D是某煤矿的四个采煤点,l是公路,图中所标线段为道路,ABQP、BCRQ、CDSR近似于正方形.已知A、B、C、D四个采煤点每天的采煤量之比约为5:1:2:3,运煤的费用与运煤的路程、所运煤的重量都成正比.现要从P、Q、R、S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在( ) (2013•房山区二模)如图,A,B,C,D是⊙O上的四个点,过点B的切线与DC的延长线交于点E.若∠BCD=110°,则∠DBE=( )
(2013•房山区二模)如图,A,B,C,D是⊙O上的四个点,过点B的切线与DC的延长线交于点E.若∠BCD=110°,则∠DBE=( )