摘要:19.设圆的方程为①2=r2与②2=r2(a=c与b=d不能同时成立),则由①式减去②式可得上述两圆的对称轴方程
网址:http://m.1010jiajiao.com/timu_id_417994[举报]
已知圆C:(x-1)2+y2=r2(r>1),设M为圆C与x轴负半轴的交点,过点M作圆C的弦MN,并使它的中点P恰好落在y轴上.
(1)当r=2时,求满足条件的P点的坐标;
(2)当r∈(1,+∞)时,求点N的轨迹E的方程;
(3)若A(x1,2)、B(x2,y2)、C(x0,y0)是E上不同的点,且AB⊥BC,求y0的取值范围.
查看习题详情和答案>>
已知圆C:(x-1)2+y2=r2(r>1),设M为圆C与x轴负半轴的交点,过点M作圆C的弦MN,并使它的中点P恰好落在y轴上.
(1)当r∈(1,+∞)时,求点N的轨迹E的方程;
(2)若A(x1,2)、B(x2,y2)、C(x0,y0)是E上不同的点,且AB⊥BC,求y0的取值范围.
查看习题详情和答案>>已知圆C:(x-1)2+y2=r2(r>1),设A为圆C与x轴负半轴的交点,过点A作圆C的弦AM,并使弦AM的中点恰好落在y轴上.
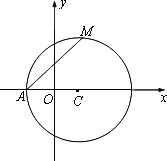
(1)当r在(1,+∞)内变化时,求点M的轨迹E的方程;
(2)设轨迹E的准线为l,N为l上的一个动点,过点N作轨迹E的两条切线,切点分别为P,Q.求证:直线PQ必经过x轴上的一个定点B,并写出点B的坐标.
 的最小值;
的最小值;