Question

已知圆C：(x－1)²＋y²＝r²(r＞1)，设A为圆C与x轴负半轴的交点，过点A作圆C的弦AM，并使弦AM的中点恰好落在y轴上．

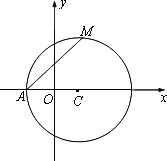
(1)当r在(1，＋∞)内变化时，求点M的轨迹E的方程；

(2)设轨迹E的准线为l，N为l上的一个动点，过点N作轨迹E的两条切线，切点分别为P，Q．求证：直线PQ必经过x轴上的一个定点B，并写出点B的坐标．

Answer 1

答案：
解析：

解：(1)设，则的中点．因为，＝(1，)，＝(x，)． 　　在⊙中，因为，所以，·＝0，所以． 　　所以，点的轨迹的方程为： 　　(2)轨迹的准线 　　所以，可设，过的斜率存在的直线方程为： 　　由得．由得：． 　　设直线，斜率分别为，，则①且， 　　所以，所以，直线的方程：． 　　令，则 　　由①知，即直线过定点．