网址:http://m.1010jiajiao.com/timu_id_35320[举报]
一、1.C 2.D 3.C 4.B 5.C 6.A 7.C 8.D 9. C 10. A
二、11. 12.
12. 13.62° 14.4 15.(n+2)2-4n=n2+4 16.25
13.62° 14.4 15.(n+2)2-4n=n2+4 16.25
17.5 18.15°或75°
 三、19.原式=a2+a-(a2-1)
……(3分)
三、19.原式=a2+a-(a2-1)
……(3分)
=a2+a-a2+1 ……(6分)
=a+1 ……(9分)
20.(1)画图如图所示; ……(4分)
(2)点A/的坐标为(-2,4); ……(7分)
(3) 的长为:
的长为: . ……(10分)
. ……(10分)
21.(1)设小明他们一共去了x个成人,则去了学生(12-x)人,依题意,得
35x+0.5×35(12-x)=350 ………………………………(3分)
解这个方程,得x=8 ………………………………(5分)
答:小明他们一共去了8个成人,去了学生4人. ……………………(6分)
(2)若按16个游客购买团体票,需付门票款为35×0.6×16=336(元) ……(8分)
∵ 336<350, ………………………………(9分)
 ∴ 按16人的团体购票更省钱.
………………………………(10分)
∴ 按16人的团体购票更省钱.
………………………………(10分)
22.(1)李华所在班级的总人数为:
14÷35%=40(人). ……(3分)
爱好书画的人数为:
40-
(2)书画部分的条形图如图所示.(9分)
(3)答案不唯一.(每写对一条给1分)如:表示“球类”的扇形圆心角为:
360× =126°爱好音乐的人数是其他爱好人数的3倍等. …………(11分)
=126°爱好音乐的人数是其他爱好人数的3倍等. …………(11分)
23.(1)由图象可知公司从第4个月末以后开始扭亏为盈. ………………………(2分)
(2)由图象可知其顶点坐标为(2,-2),
故可设其函数关系式为:y=a(t-2)2-2. ………………………………(4分)
∵ 所求函数关系式的图象过(0,0),于是得
a(0-2)2-2=0,解得a= .
………………………………(5分)
.
………………………………(5分)
∴ 所求函数关系式为:S= (t-2)2-2或S=
(t-2)2-2或S= t2-2t. ………………………(7分)
t2-2t. ………………………(7分)
(3)把t=7代入关系式,得S= ×72-2×7=10.5 ……………………………(10分)
×72-2×7=10.5 ……………………………(10分)
把t=8代入关系式,得S= ×82-2×8=16
×82-2×8=16
16-10.5=5.5 ………………………………(11分)
答:第8个月公司所获利是5.5万元. ………………………………(12分)
24.(1)∵ BC、DE分别是两个等腰直角△ADE、△ABC的斜边,
∴ ∠DAE=∠BAC=90°,
∴ ∠DAE-∠DAC=∠BAC-∠DAC,∴ ∠CAE=∠BAD. ………………(2分)
在△ACE和△ABD中,
 ………………………………(4分)
………………………………(4分)
∴ △ACE≌△ABD(S?A?S). ………………………………(5分)
(2)①∵ AC=AB= ,
,
∴ BC=AC2+AB2= ,
,
∴ BC=4. ………………………………(6分)
∵ AB=AC, ∠BAC=90°,
∴ ∠ACB=∠B=45°,
∵ △ACE≌△ABD
∴ ∠ACB=∠B=45°
∴ ∠DCE=90°. ………………………………(7分)
∵ △ACE≌△ABD,
∴ CE=BD=x,而BC=4,∴ DC=4-x,
∴ Rt△DCE的面积为 DC?CE=
DC?CE= (4-x)x.
(4-x)x.
∴  (4-x)x=1.5
………………………………(9分)
(4-x)x=1.5
………………………………(9分)
即x2-4x+3=0. 解得x=1或x=3. ………………………………(11分)
② △DCE存在最大值,理由如下:
设△DCE的面积为y,于是得y与x的函数关系式为:
y= (4-x)x (0<x<4)
………………………………(12分)
(4-x)x (0<x<4)
………………………………(12分)
=- (x-2)2+2
(x-2)2+2
∵ a=- <0, ∴ 当x=2时,函数y有最大值2. ……………………(13分)
<0, ∴ 当x=2时,函数y有最大值2. ……………………(13分)
又∵ 此时,x满足关系式0<x<4,
故当x=2时,△DCE的最大面积为2. ………………………………(14分)
(1)若c=2b-1,点M在x轴上,求c的值.
(2)若直线y=-
| 1 | 2 |
 (2,0)、(1,3
(2,0)、(1,3| 3 |
| 3 |
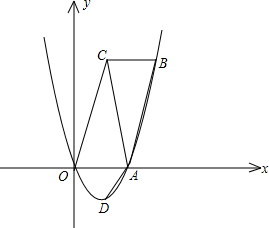
(1)求证:四边形ABCO是平行四边形;
(2)求a的值并说明点B在抛物线上;
(3)若点P是线段OA上一点,且∠APD=∠OAB,求点P的坐标;
(4)若点P是x轴上一点,以P、A、D为顶点作平行四边形,该平行四边形的另一顶点在y轴上,写出点P的坐标. 查看习题详情和答案>>
| 1 | 4 |
(1)求抛物线的函数解析式和点E的坐标;
(2)求证:ME是⊙P的切线;
(3)如图(2),点R从正方形CDEF的顶点E出发以1个单位/秒的速度向点F运动,同时点S从点Q出发沿y轴以5个单位/秒的速度向上运动,连接RS,设运动时间为t秒(0<t<1),在运动过程中,正方形CDEF在直线RS下方部分的面积是否变化?若不变,说明理由并求出其值;若变化,请说明理由;
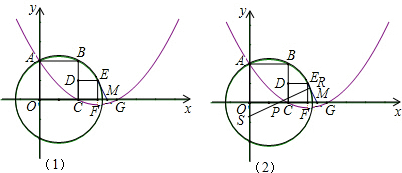
| 1 |
| 2 |
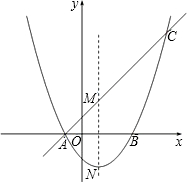 对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.
对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.(1)求这条抛物线的函数关系式;
(2)设题中的抛物线与直线的另一交点为C,已知P为线段AC上一点(不含端点),过点P作PQ⊥x轴,交抛物线于点Q,试证明:当P为AC的中点时,线段PQ的长取得最大值,并求出PQ的最大值;
(3)设D、E为直线AC上的两点(不与A、C重合),且D在E的左侧,DE=2
| 2 |
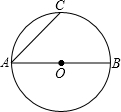 如图,AB为⊙O的直径,其长度为2cm,点C为半圆弧的中点,若⊙O的另一条弦AD长等于
如图,AB为⊙O的直径,其长度为2cm,点C为半圆弧的中点,若⊙O的另一条弦AD长等于