题目内容
如图,抛物线y=| 1 |
| 2 |
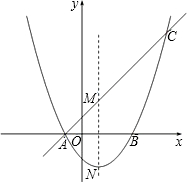 对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.
对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.(1)求这条抛物线的函数关系式;
(2)设题中的抛物线与直线的另一交点为C,已知P为线段AC上一点(不含端点),过点P作PQ⊥x轴,交抛物线于点Q,试证明:当P为AC的中点时,线段PQ的长取得最大值,并求出PQ的最大值;
(3)设D、E为直线AC上的两点(不与A、C重合),且D在E的左侧,DE=2
| 2 |
分析:(1)由于点M和抛物线顶点关于x轴对称,即可得到点N的坐标,进而表示出该抛物线的顶点坐标式函数解析式.
(2)根据(1)所得抛物线的解析式,可得到点A的坐标,进而可求出直线AC的解析式,设出点P的横坐标,根据直线AC和抛物线的解析式,即可得到P、Q的纵坐标,从而得到关于PQ的长和P点横坐标的函数关系式,根据所得函数的性质即可求出PQ的最大值及对应的P点坐标,然后判断此时的P点是否为AC的中点即可.
(3)由直线AC的斜率可得∠CAB=45°,因此D、E的横坐标差为2,可设出点D的横坐标,即可得到点E的横坐标,进而可参照(2)的方法求得DF、EG的长,若以D、E、F、G为顶点的四边形为平行四边形,那么必须满足DE=FG,由此可求得点D的坐标.需要注意的是:在表示DE、FG的长时,要分三种情况考虑:
①点D在线段CA的延长线上,E在线段AC上,②D、E都在线段AC上,③点E在线段AC的延长线上,D在线段AC上.
(2)根据(1)所得抛物线的解析式,可得到点A的坐标,进而可求出直线AC的解析式,设出点P的横坐标,根据直线AC和抛物线的解析式,即可得到P、Q的纵坐标,从而得到关于PQ的长和P点横坐标的函数关系式,根据所得函数的性质即可求出PQ的最大值及对应的P点坐标,然后判断此时的P点是否为AC的中点即可.
(3)由直线AC的斜率可得∠CAB=45°,因此D、E的横坐标差为2,可设出点D的横坐标,即可得到点E的横坐标,进而可参照(2)的方法求得DF、EG的长,若以D、E、F、G为顶点的四边形为平行四边形,那么必须满足DE=FG,由此可求得点D的坐标.需要注意的是:在表示DE、FG的长时,要分三种情况考虑:
①点D在线段CA的延长线上,E在线段AC上,②D、E都在线段AC上,③点E在线段AC的延长线上,D在线段AC上.
解答:解:(1)由题意知,抛物线顶点N的坐标为(1,-2),(1分)
∴其函数关系式为y=
(x-1)2-2=
x2-x-
.(3分)
(2)由
x2-x-
=0
得x=-1或3,即A(-1,0)、B(3,0);
由A(-1,0)、M(1,2)可得直线AC的函数关系式为y=x+1,(4分)
设P(t,t+1),则Q的坐标为(t,
t2-t-
);(5分)
∴PQ=(t+1)-(
t2-t-
)=-
t2+2t+
=-
(t-2)2+
,(6分)
∵a=-
<0
∴当t=2时,PQ有最大值为
,
即P点运动至AC的中点时,PQ长有最大值为
.(7分)
(3)由直线AC的函数关系式为y=x+1可知:∠CAB=45°,则D、E的横坐标差为2;
设点D(x,x+1),E(x+2,x+3),则:F(x,
x2-x-
),G(x+2,
x2+x-
);
由于DF∥EG,若以D、E、F、G为顶点的四边形为平行四边形,则DF=EG;
①当点D在线段CA的延长线上,点E在线段AC上时;
DF=
x2-x-
-(x+1)=
x2-2x-
,EG=x+3-(
x2+x-
)=-
x2+
;
由于DF=EG,则
x2-2x-
=-
x2+
,
解得x=1±2
;
由于x<0,则D(1-2
,2-2
);
②当点D、E都在线段AC上时;
DF=-
x2+2x+
,EG=-
x2+
;
同①可得:-
x2+2x+
=-
x2+
,
解得x=1;
故D(1,2);
③当点D在线段AC上,E点在线段AC的延长线上时,
DF=
x2-x-
-(x+1)=
x2-2x-
,EG=x+3-(
x2+x-
)=-
x2+
;
由于DF=EG,则
x2-2x-
=-
x2+
,
解得x=1±2
;
由于x>0,则D(1+2
,2+2
);
符合条件的点共有3个,分别为D1(1,2),D2(1-2
,2-2
),D3(1+2
,2+2
).(11分)
(第(3)小题得出1解得(2分),2解得(3分),3解得4分)
∴其函数关系式为y=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
(2)由
| 1 |
| 2 |
| 3 |
| 2 |
得x=-1或3,即A(-1,0)、B(3,0);
由A(-1,0)、M(1,2)可得直线AC的函数关系式为y=x+1,(4分)
设P(t,t+1),则Q的坐标为(t,
| 1 |
| 2 |
| 3 |
| 2 |
∴PQ=(t+1)-(
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
∵a=-
| 1 |
| 2 |
∴当t=2时,PQ有最大值为
| 9 |
| 2 |
即P点运动至AC的中点时,PQ长有最大值为
| 9 |
| 2 |
(3)由直线AC的函数关系式为y=x+1可知:∠CAB=45°,则D、E的横坐标差为2;
设点D(x,x+1),E(x+2,x+3),则:F(x,
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
由于DF∥EG,若以D、E、F、G为顶点的四边形为平行四边形,则DF=EG;
①当点D在线段CA的延长线上,点E在线段AC上时;
DF=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
由于DF=EG,则
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
解得x=1±2
| 2 |
由于x<0,则D(1-2
| 2 |
| 2 |
②当点D、E都在线段AC上时;
DF=-
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
同①可得:-
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
解得x=1;
故D(1,2);
③当点D在线段AC上,E点在线段AC的延长线上时,
DF=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
由于DF=EG,则
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
解得x=1±2
| 2 |
由于x>0,则D(1+2
| 2 |
| 2 |
符合条件的点共有3个,分别为D1(1,2),D2(1-2
| 2 |
| 2 |
| 2 |
| 2 |
(第(3)小题得出1解得(2分),2解得(3分),3解得4分)
点评:此题主要考查了二次函数解析式的确定、函数图象交点坐标的求法、二次函数最值的应用、平行四边形的判定和性质等知识,同时考虑了分类讨论的数学思想,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,抛物线y=ax2+bx+c与x轴交于点A、B,与y轴交于点C,如果OB=OC=
如图,抛物线y=ax2+bx+c与x轴交于点A、B,与y轴交于点C,如果OB=OC=| 1 |
| 2 |
| A、-2 | ||
| B、-1 | ||
C、-
| ||
D、
|
 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 已知:如图,抛物线y=x2+bx+c(b、c为常数)经过原点和E(3,0).
已知:如图,抛物线y=x2+bx+c(b、c为常数)经过原点和E(3,0). 如图,抛物线
如图,抛物线 如图,抛物线y=ax2+bx+
如图,抛物线y=ax2+bx+