ĖâÄŋÄÚČÝ
ČįÍžĢŽÔÚÆ―ÃæÖą―ĮŨøąęÏĩxOyÖÐĢŽOΊÔĩãĢŽĩãAĄĒCĩÄŨøąę·ÖąðΊ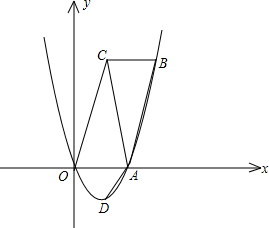 ĢĻ2ĢŽ0ĢĐĄĒĢĻ1ĢŽ3
ĢĻ2ĢŽ0ĢĐĄĒĢĻ1ĢŽ3| 3 |
| 3 |
ĢĻ1ĢĐĮóÖĪĢšËÄąßÐÎABCOĘĮÆ―ÐÐËÄąßÐÎĢŧ
ĢĻ2ĢĐĮóaĩÄÖĩēĒËĩÃũĩãBÔÚÅŨÎïÏßÉÏĢŧ
ĢĻ3ĢĐČôĩãPĘĮÏßķÎOAÉÏŌŧĩãĢŽĮŌĄÏAPD=ĄÏOABĢŽĮóĩãPĩÄŨøąęĢŧ
ĢĻ4ĢĐČôĩãPĘĮxÖáÉÏŌŧĩãĢŽŌÔPĄĒAĄĒDΊķĨĩãŨũÆ―ÐÐËÄąßÐÎĢŽļÃÆ―ÐÐËÄąßÐÎĩÄÁíŌŧķĨĩãÔÚyÖáÉÏĢŽÐīģöĩãPĩÄŨøąęĢŪ
·ÖÎöĢšĢĻ1ĢĐÓÉÐýŨŠĩÄÐÔÖĘŋÉÖŠĢšĄũAOCĄÕĄũABCĢŽÓÉīËŋÉĩÃģöËÄąßÐÎAOCBĩÄÁ―ŨéķÔąß·ÖąðķÔÓĶÏāĩČĢŪÓÉīËŋÉĩÃÖĪĢŪ
ĢĻ2ĢĐÓÉÓÚÅŨÎïÏßđýAĩãĢŽŌōīËŋÉ―ŦAĩãĩÄŨøąęīúČëÅŨÎïÏßĩÄ―âÎöĘ―ÖОīŋÉĩÃģöaĩÄÖĩšÍÅŨÎïÏßĩÄ―âÎöĘ―ĢŪ
ŌŠÅÐķÏBĘĮ·ņÔÚÅŨÎïÏßĩÄ―âÎöĘ―ÉÏĢŽĘŨÏČŌŠĮóģöBĩãĩÄŨøąęĢŽÓÉÓÚËÄąßÐÎAPCBĘĮÆ―ÐÐËÄąßÐÎĢŽOA=2ĢŽŌōīË―ŦCĩãÏōÓŌÆ―ŌÆ2ļöĩĨÎŧžīŋÉĩÃģöBĩãĩÄŨøąęĢŽČŧšó―ŦBĩÄŨøąęīúČëÅŨÎïÏßĩÄ―âÎöĘ―ÖОīŋÉÅÐķÏģöBĘĮ·ņÔÚÅŨÎïÏßÉÏĢŪ
ĢĻ3ĢĐÏČļųūÝĢĻ2ĢĐĩÄÅŨÎïÏßĩÄ―âÎöĘ―ĮóģöķĨĩãDĩÄŨøąęĢŽČŧšóĮóģöOBĄĒADĩÄģĪĢŽĩąĄÏAPD=ĄÏOABĘąĢŽŋÉĩÃģöĄũAPDĄŨĄũOABĢŽ―øķøŋÉĩÃģöđØÓÚAPĢŽADĄĒOAĄĒOBĩÄąČĀýđØÏĩĘ―ĢŪÉčģöPĩãĩÄŨøąęĢŽČŧšóÓÃPĩÄšáŨøąęąíĘūģöAPĩÄģĪĢŽžīŋÉļųūÝÉÏÃæĩÄąČĀýđØÏĩĘ―ĮóģöPĩãĩÄŨøąęĢŪ
ĢĻ4ĢĐĒŲČįĩÚŌŧļöÍžĢšīËĘąQD=AP=1ĢŽŌōīËOP=OA-1=1ĢŽPĩãĩÄŨøąęΊĢĻ1ĢŽ0ĢĐĢŧ
ĒÚČįĩÚķþļöÍžĢšīËĘąOP=OA+AP=3ĢŽPĩãĩÄŨøąęΊĢĻ3ĢŽ0ĢĐĢŧ
ĒÛČįĩÚČýļöÍžĢšīËĘąDĢŽQÁ―ĩãĩÄŨÝŨøąęŧĨΊÏā·īĘýĢŽŌōīËQĩãĩÄŨøąęΊĢĻ0ĢŽ
ĢĐĢŽļųūÝAĢŽDĩÄŨøąęŋÉĮóģöÖąÏßADĩÄ―âÎöĘ―ÎŠy=
x-2
ĢŽÓÉÓÚQPĄÎADĢŽŌōīËÖąÏßPQĩÄ―âÎöĘ―ÎŠy=
x+
ĢŽŋÉĮóĩÃPĩãĩÄŨøąęΊĢĻ-1ĢŽ0ĢĐĢŪ
ĢĻ2ĢĐÓÉÓÚÅŨÎïÏßđýAĩãĢŽŌōīËŋÉ―ŦAĩãĩÄŨøąęīúČëÅŨÎïÏßĩÄ―âÎöĘ―ÖОīŋÉĩÃģöaĩÄÖĩšÍÅŨÎïÏßĩÄ―âÎöĘ―ĢŪ
ŌŠÅÐķÏBĘĮ·ņÔÚÅŨÎïÏßĩÄ―âÎöĘ―ÉÏĢŽĘŨÏČŌŠĮóģöBĩãĩÄŨøąęĢŽÓÉÓÚËÄąßÐÎAPCBĘĮÆ―ÐÐËÄąßÐÎĢŽOA=2ĢŽŌōīË―ŦCĩãÏōÓŌÆ―ŌÆ2ļöĩĨÎŧžīŋÉĩÃģöBĩãĩÄŨøąęĢŽČŧšó―ŦBĩÄŨøąęīúČëÅŨÎïÏßĩÄ―âÎöĘ―ÖОīŋÉÅÐķÏģöBĘĮ·ņÔÚÅŨÎïÏßÉÏĢŪ
ĢĻ3ĢĐÏČļųūÝĢĻ2ĢĐĩÄÅŨÎïÏßĩÄ―âÎöĘ―ĮóģöķĨĩãDĩÄŨøąęĢŽČŧšóĮóģöOBĄĒADĩÄģĪĢŽĩąĄÏAPD=ĄÏOABĘąĢŽŋÉĩÃģöĄũAPDĄŨĄũOABĢŽ―øķøŋÉĩÃģöđØÓÚAPĢŽADĄĒOAĄĒOBĩÄąČĀýđØÏĩĘ―ĢŪÉčģöPĩãĩÄŨøąęĢŽČŧšóÓÃPĩÄšáŨøąęąíĘūģöAPĩÄģĪĢŽžīŋÉļųūÝÉÏÃæĩÄąČĀýđØÏĩĘ―ĮóģöPĩãĩÄŨøąęĢŪ
ĢĻ4ĢĐĒŲČįĩÚŌŧļöÍžĢšīËĘąQD=AP=1ĢŽŌōīËOP=OA-1=1ĢŽPĩãĩÄŨøąęΊĢĻ1ĢŽ0ĢĐĢŧ
ĒÚČįĩÚķþļöÍžĢšīËĘąOP=OA+AP=3ĢŽPĩãĩÄŨøąęΊĢĻ3ĢŽ0ĢĐĢŧ
ĒÛČįĩÚČýļöÍžĢšīËĘąDĢŽQÁ―ĩãĩÄŨÝŨøąęŧĨΊÏā·īĘýĢŽŌōīËQĩãĩÄŨøąęΊĢĻ0ĢŽ
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
―âīðĢš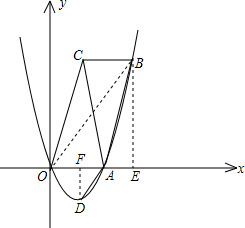 ĢĻ1ĢĐÖĪÃũĢšĄßĄũAOCČÆACĩÄÖÐĩãÐýŨŠ180ĄãĢŽ
ĢĻ1ĢĐÖĪÃũĢšĄßĄũAOCČÆACĩÄÖÐĩãÐýŨŠ180ĄãĢŽ
ĩãOÂäĩ―ĩãBĩÄÎŧÖÃĢŽ
ĄāĄũACOĄÕĄũCABĢŪ
ĄāAO=CBĢŽCO=ABĢŽ
ĄāËÄąßÐÎABCOĘĮÆ―ÐÐËÄąßÐÎĢŪ
ĢĻ2ĢĐ―âĢšĄßÅŨÎïÏßy=ax2-2
xūđýĩãAĢŽ
ĩãAĩÄŨøąęΊĢĻ2ĢŽ0ĢĐĢŽ
Ąā4a-4
=0ĢŽ
―âĩÃĢša=
ĢŪ
Ąāy=
x2-2
xĢŪ
ĄßËÄąßÐÎABCOĘĮÆ―ÐÐËÄąßÐÎĢŽ
ĄāOAĄÎCBĢŪ
ĄßĩãCĩÄŨøąęΊĢĻ1ĢŽ3
ĢĐĢŽ
ĄāĩãBĩÄŨøąęΊĢĻ3ĢŽ3
ĢĐĢŪ
°Ņx=3īúČëīËšŊĘý―âÎöĘ―ĢŽĩÃĢšy=
ĄÁ32-2
ĄÁ3=3
ĢŪ
ĄāĩãBĩÄŨøąęÂúŨãīËšŊĘý―âÎöĘ―ĢŽĩãBÔÚīËÅŨÎïÏßÉÏĢŪ
ĄāķĨĩãDĩÄŨøąęΊĢĻ1ĢŽ-
ĢĐĢŪ
ĢĻ3ĢĐÁŽ―ÓBOĢŽ
đýĩãBŨũBEĄÍxÖáÓÚĩãEĢŽ
đýĩãDŨũDFĄÍxÖáÓÚĩãFĢŪ
tanĄÏBOE=
ĢŽtanĄÏDAF=
ĢŽ
ĄātanĄÏBOE=tanĄÏDAFĢŪ
ĄāĄÏBOE=ĄÏDAFĢŪ
ĄßĄÏAPD=ĄÏOABĢŽ
ĄāĄũAPDĄŨĄũOABĢŪ
ÉčĩãPĩÄŨøąęΊĢĻxĢŽ0ĢĐĢŽ
Ąā
=
ĢŽ
Ąā
=
ĢŽ
―âĩÃĢšx=
ĢŪ
ĄāĩãPĩÄŨøąęΊĢĻ
ĢŽ0ĢĐĢŪ
ĢĻ4ĢĐ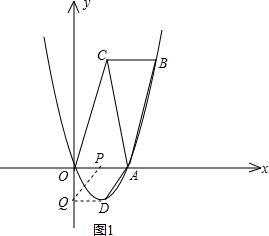
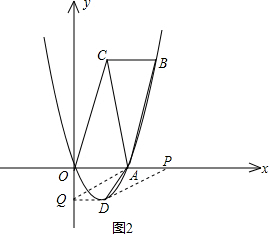
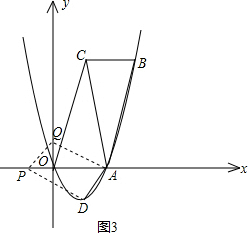
·ÖČýÖÖĮéŋö―øÐÐĖÖÂÛĢš
ĒŲČįĩÚŌŧļöÍžĢšīËĘąQD=AP=1ĢŽŌōīËOP=OA-1=1ĢŽPĩãĩÄŨøąęΊĢĻ1ĢŽ0ĢĐĢŧ
ĒÚČįĩÚķþļöÍžĢšīËĘąOP=OA+AP=3ĢŽPĩãĩÄŨøąęΊĢĻ3ĢŽ0ĢĐĢŧ
ĒÛČįĩÚČýļöÍžĢšīËĘąDĢŽQÁ―ĩãĩÄŨÝŨøąęŧĨΊÏā·īĘýĢŽŌōīËQĩãĩÄŨøąęΊĢĻ0ĢŽ
ĢĐĢŽļųūÝAĢŽDĩÄŨøąęŋÉĮóģöÖąÏßADĩÄ―âÎöĘ―ÎŠy=
x-2
ĢŽÓÉÓÚQPĄÎADĢŽŌōīËÖąÏßPQĩÄ―âÎöĘ―ÎŠy=
x+
ĢŽŋÉĮóĩÃPĩãĩÄŨøąęΊĢĻ-1ĢŽ0ĢĐĢŪ
ŨÛÉÏËųĘöĢŽđēÓÐ3ļö·ûšÏĖõžþĩÄPĩãĩÄŨøąęĢŽžīP1ĢĻ1ĢŽ0ĢĐĢŽP2ĢĻ-1ĢŽ0ĢĐĢŽP3ĢĻ3ĢŽ0ĢĐĢŪ
 ĢĻ1ĢĐÖĪÃũĢšĄßĄũAOCČÆACĩÄÖÐĩãÐýŨŠ180ĄãĢŽ
ĢĻ1ĢĐÖĪÃũĢšĄßĄũAOCČÆACĩÄÖÐĩãÐýŨŠ180ĄãĢŽĩãOÂäĩ―ĩãBĩÄÎŧÖÃĢŽ
ĄāĄũACOĄÕĄũCABĢŪ
ĄāAO=CBĢŽCO=ABĢŽ
ĄāËÄąßÐÎABCOĘĮÆ―ÐÐËÄąßÐÎĢŪ
ĢĻ2ĢĐ―âĢšĄßÅŨÎïÏßy=ax2-2
| 3 |
ĩãAĩÄŨøąęΊĢĻ2ĢŽ0ĢĐĢŽ
Ąā4a-4
| 3 |
―âĩÃĢša=
| 3 |
Ąāy=
| 3 |
| 3 |
ĄßËÄąßÐÎABCOĘĮÆ―ÐÐËÄąßÐÎĢŽ
ĄāOAĄÎCBĢŪ
ĄßĩãCĩÄŨøąęΊĢĻ1ĢŽ3
| 3 |
ĄāĩãBĩÄŨøąęΊĢĻ3ĢŽ3
| 3 |
°Ņx=3īúČëīËšŊĘý―âÎöĘ―ĢŽĩÃĢšy=
| 3 |
| 3 |
| 3 |
ĄāĩãBĩÄŨøąęÂúŨãīËšŊĘý―âÎöĘ―ĢŽĩãBÔÚīËÅŨÎïÏßÉÏĢŪ
ĄāķĨĩãDĩÄŨøąęΊĢĻ1ĢŽ-
| 3 |
ĢĻ3ĢĐÁŽ―ÓBOĢŽ
đýĩãBŨũBEĄÍxÖáÓÚĩãEĢŽ
đýĩãDŨũDFĄÍxÖáÓÚĩãFĢŪ
tanĄÏBOE=
| 3 |
| 3 |
ĄātanĄÏBOE=tanĄÏDAFĢŪ
ĄāĄÏBOE=ĄÏDAFĢŪ
ĄßĄÏAPD=ĄÏOABĢŽ
ĄāĄũAPDĄŨĄũOABĢŪ
ÉčĩãPĩÄŨøąęΊĢĻxĢŽ0ĢĐĢŽ
Ąā
| AP |
| OA |
| AD |
| OB |
Ąā
| 2-x |
| 2 |
| 2 |
| 6 |
―âĩÃĢšx=
| 4 |
| 3 |
ĄāĩãPĩÄŨøąęΊĢĻ
| 4 |
| 3 |
ĢĻ4ĢĐ



·ÖČýÖÖĮéŋö―øÐÐĖÖÂÛĢš
ĒŲČįĩÚŌŧļöÍžĢšīËĘąQD=AP=1ĢŽŌōīËOP=OA-1=1ĢŽPĩãĩÄŨøąęΊĢĻ1ĢŽ0ĢĐĢŧ
ĒÚČįĩÚķþļöÍžĢšīËĘąOP=OA+AP=3ĢŽPĩãĩÄŨøąęΊĢĻ3ĢŽ0ĢĐĢŧ
ĒÛČįĩÚČýļöÍžĢšīËĘąDĢŽQÁ―ĩãĩÄŨÝŨøąęŧĨΊÏā·īĘýĢŽŌōīËQĩãĩÄŨøąęΊĢĻ0ĢŽ
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
ŨÛÉÏËųĘöĢŽđēÓÐ3ļö·ûšÏĖõžþĩÄPĩãĩÄŨøąęĢŽžīP1ĢĻ1ĢŽ0ĢĐĢŽP2ĢĻ-1ĢŽ0ĢĐĢŽP3ĢĻ3ĢŽ0ĢĐĢŪ
ĩãÆĀĢšąūĖâŨÅÖØŋžēéÁËīýķĻÏĩĘý·ĻĮóķþīΚŊĘý―âÎöĘ―ĄĒÍžÐÎÐýŨŠąäŧŧĄĒČý―ĮÐÎÏāËÆĄĒÆ―ÐÐËÄąßÐÎĩÄÅÐķĻĩČÖŠĘķĩãĢŽŨÛšÏÐÔĮŋĢŽŋžēéŅ§Éú·ÖĀāĖÖÂÛĢŽĘýÐÎ―ášÏĩÄĘýŅ§ËžÏë·―·ĻĢŪ

Á·Ï°ēáÏĩÁÐīð°ļ
ÏāđØĖâÄŋ
 ČįÍžĢŽÔÚÆ―ÃæÖą―ĮŨøąęÖÐĢŽËÄąßÐÎOABCĘĮĩČŅüĖÝÐÎĢŽCBĄÎOAĢŽOA=7ĢŽAB=4ĢŽĄÏCOA=60ĄãĢŽĩãPΊxÖáÉÏĩÄŌŧļöķŊĩãĢŽĩŦĘĮĩãPēŧÓëĩã0ĄĒĩãAÖØšÏĢŪÁŽ―ÓCPĢŽDĩãĘĮÏßķÎABÉÏŌŧĩãĢŽÁŽ―ÓPDĢŪ
ČįÍžĢŽÔÚÆ―ÃæÖą―ĮŨøąęÖÐĢŽËÄąßÐÎOABCĘĮĩČŅüĖÝÐÎĢŽCBĄÎOAĢŽOA=7ĢŽAB=4ĢŽĄÏCOA=60ĄãĢŽĩãPΊxÖáÉÏĩÄŌŧļöķŊĩãĢŽĩŦĘĮĩãPēŧÓëĩã0ĄĒĩãAÖØšÏĢŪÁŽ―ÓCPĢŽDĩãĘĮÏßķÎABÉÏŌŧĩãĢŽÁŽ―ÓPDĢŪ ĢĻ2012•ÓåąąĮøŌŧÄĢĢĐČįÍžĢŽÔÚÆ―ÃæÖą―ĮŨøąęxoyÖÐĢŽŌÔŨøąęÔĩãOΊÔēÐÄĢŽ3Ί°ëūķŧÔēĢŽīÓīËÔēÄÚĢĻ°üĀĻąß―įĢĐĩÄËųÓÐÕûĘýĩãĢĻšáĄĒŨÝŨøąęūųΊÕûĘýĢĐÖÐČÎŌâŅĄČĄŌŧļöĩãĢŽÆäšáĄĒŨÝŨøąęÖŪšÍΊ0ĩÄļÅÂĘĘĮ
ĢĻ2012•ÓåąąĮøŌŧÄĢĢĐČįÍžĢŽÔÚÆ―ÃæÖą―ĮŨøąęxoyÖÐĢŽŌÔŨøąęÔĩãOΊÔēÐÄĢŽ3Ί°ëūķŧÔēĢŽīÓīËÔēÄÚĢĻ°üĀĻąß―įĢĐĩÄËųÓÐÕûĘýĩãĢĻšáĄĒŨÝŨøąęūųΊÕûĘýĢĐÖÐČÎŌâŅĄČĄŌŧļöĩãĢŽÆäšáĄĒŨÝŨøąęÖŪšÍΊ0ĩÄļÅÂĘĘĮ ČįÍžĢŽÔÚÆ―ÃæÖą―ĮŨøąęÖÐĢŽĩČŅüĖÝÐÎABCDĩÄÏÂĩŨÔÚxÖáÉÏĢŽĮŌBĩãŨøąęΊĢĻ4ĢŽ0ĢĐĢŽDĩãŨøąęΊĢĻ0ĢŽ3ĢĐĢŽÔōACģĪΊ
ČįÍžĢŽÔÚÆ―ÃæÖą―ĮŨøąęÖÐĢŽĩČŅüĖÝÐÎABCDĩÄÏÂĩŨÔÚxÖáÉÏĢŽĮŌBĩãŨøąęΊĢĻ4ĢŽ0ĢĐĢŽDĩãŨøąęΊĢĻ0ĢŽ3ĢĐĢŽÔōACģĪΊ ČįÍžĢŽÔÚÆ―ÃæÖą―ĮŨøąęxOyÖÐĢŽŌŅÖŠĩãAĢĻ-5ĢŽ0ĢĐĢŽPĘĮ·īąČĀýšŊĘý
ČįÍžĢŽÔÚÆ―ÃæÖą―ĮŨøąęxOyÖÐĢŽŌŅÖŠĩãAĢĻ-5ĢŽ0ĢĐĢŽPĘĮ·īąČĀýšŊĘý ĄÏCOA=45ĄãĢŽķŊĩãPīÓĩãOģö·ĒĢŽÔÚĖÝÐÎOABCĩÄąßÉÏÔËķŊĢŽÂ·ūķΊOĄúAĄúBĄúCĢŽĩ―īïĩãCĘąÍĢÖđĢŪŨũÖąÏßCPĢŪ
ĄÏCOA=45ĄãĢŽķŊĩãPīÓĩãOģö·ĒĢŽÔÚĖÝÐÎOABCĩÄąßÉÏÔËķŊĢŽÂ·ūķΊOĄúAĄúBĄúCĢŽĩ―īïĩãCĘąÍĢÖđĢŪŨũÖąÏßCPĢŪ