摘要：21．(Ⅰ)由2 an+1 = 3an-an-1.得 2(an+1-an)= an-an-1.
网址：http://m.1010jiajiao.com/timu_id_34916[举报]
对于数列{an}，若存在确定的自然数T＞0，使得对任意的自然数n∈N*，都有：an+T=an成立，则称数列{an}是以T为周期的周期数列．
（1）记Sn=a1+a2+a3+…+an，若{an}满足an+2=an+1-an，且S2=1007，S3=2010，求证：数列{an}是以6为周期的周期数列，并求S2009；
（2）若{an}满足a1=p∈[0，
)，且an+1=-2an2+2an，试判断{an}是否为周期数列，且说明理由；
（3）由（1）得数列{an}，又设数列{bn}，其中bn=an+2n+
，问是否存在最小的自然数n（n∈N*），使得对一切自然数m≥n，都有bm＞2009？请说明理由．
查看习题详情和答案>>
（1）记Sn=a1+a2+a3+…+an，若{an}满足an+2=an+1-an，且S2=1007，S3=2010，求证：数列{an}是以6为周期的周期数列，并求S2009；
（2）若{an}满足a1=p∈[0，
| 1 |
| 2 |
（3）由（1）得数列{an}，又设数列{bn}，其中bn=an+2n+
| 2009 |
| 2n |
对于数列{an}，若存在确定的自然数T＞0，使得对任意的自然数n∈N*，都有：an+T=an成立，则称数列{an}是以T为周期的周期数列．
（1）记Sn=a1+a2+a3+…+an，若{an}满足an+2=an+1-an，且S2=1007，S3=2010，求证：数列{an}是以6为周期的周期数列，并求S2009；
（2）若{an}满足
，且an+1=-2an2+2an，试判断{an}是否为周期数列，且说明理由；
（3）由（1）得数列{an}，又设数列{bn}，其中
，问是否存在最小的自然数n（n∈N*），使得对一切自然数m≥n，都有bm＞2009？请说明理由．
查看习题详情和答案>>
（1）记Sn=a1+a2+a3+…+an，若{an}满足an+2=an+1-an，且S2=1007，S3=2010，求证：数列{an}是以6为周期的周期数列，并求S2009；
（2）若{an}满足
，且an+1=-2an2+2an，试判断{an}是否为周期数列，且说明理由；（3）由（1）得数列{an}，又设数列{bn}，其中
，问是否存在最小的自然数n（n∈N*），使得对一切自然数m≥n，都有bm＞2009？请说明理由．查看习题详情和答案>>
对于数列{an}，若存在确定的自然数T＞0，使得对任意的自然数n∈N*，都有：an+T=an成立，则称数列{an}是以T为周期的周期数列．
（1）记Sn=a1+a2+a3+…+an，若{an}满足an+2=an+1-an，且S2=1007，S3=2010，求证：数列{an}是以6为周期的周期数列，并求S2009；
（2）若{an}满足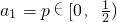
，且an+1=-2an2+2an，试判断{an}是否为周期数列，且说明理由；
（3）由（1）得数列{an}，又设数列{bn}，其中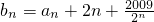
，问是否存在最小的自然数n（n∈N*），使得对一切自然数m≥n，都有bm＞2009？请说明理由．
查看习题详情和答案>>
对于数列{an}，若存在确定的自然数T＞0，使得对任意的自然数n∈N*，都有：an+T=an成立，则称数列{an}是以T为周期的周期数列．
（1）记Sn=a1+a2+a3+…+an，若{an}满足an+2=an+1-an，且S2=1007，S3=2010，求证：数列{an}是以6为周期的周期数列，并求S2009；
（2）若{an}满足a1=p∈[0，
)，且an+1=-2an2+2an，试判断{an}是否为周期数列，且说明理由；
（3）由（1）得数列{an}，又设数列{bn}，其中bn=an+2n+
，问是否存在最小的自然数n（n∈N*），使得对一切自然数m≥n，都有bm＞2009？请说明理由．
查看习题详情和答案>>
（1）记Sn=a1+a2+a3+…+an，若{an}满足an+2=an+1-an，且S2=1007，S3=2010，求证：数列{an}是以6为周期的周期数列，并求S2009；
（2）若{an}满足a1=p∈[0，
| 1 |
| 2 |
（3）由（1）得数列{an}，又设数列{bn}，其中bn=an+2n+
| 2009 |
| 2n |