题目内容
对于数列{an},若存在确定的自然数T>0,使得对任意的自然数n∈N*,都有:an+T=an成立,则称数列{an}是以T为周期的周期数列.(1)记Sn=a1+a2+a3+…+an,若{an}满足an+2=an+1-an,且S2=1007,S3=2010,求证:数列{an}是以6为周期的周期数列,并求S2009;
(2)若{an}满足
 ,且an+1=-2an2+2an,试判断{an}是否为周期数列,且说明理由;
,且an+1=-2an2+2an,试判断{an}是否为周期数列,且说明理由;(3)由(1)得数列{an},又设数列{bn},其中
 ,问是否存在最小的自然数n(n∈N*),使得对一切自然数m≥n,都有bm>2009?请说明理由.
,问是否存在最小的自然数n(n∈N*),使得对一切自然数m≥n,都有bm>2009?请说明理由.
【答案】分析:(1)an+6=an+5-an-4=an+4-an+3-an-4=-an+3=-an+2+an+1=-(an+1-an)+an+1=an,得T=6,由此能求出 S2009=S5=a3=1003.
(2)当p=0时,a1=a2=0,an+1=-2an2+2an=0,即{an}是周期数列,由此能推导出数列{an}是递增数列,非周期数列.
(3)由S2=a1+a2=a1+1005=1007,知a1=2,a2=1005,a3=1003,a4=-2,a5=-1005,a6=-1003,且数列{an}是周期为6的周期数列,由此能推导出存在最小的自然数n=1506,对一切自然数m,当m≥n=1506,都有bm>2009.
解答:解:(1)an+6=an+5-an-4=an+4-an+3-an-4
=-an+3=-an+2+an+1=-(an+1-an)+an+1=an,
得T=6
所以,数列{an}是以6为周期的周期数列,
周期为任意正整数--(2分)
又由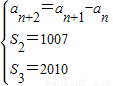 ,
,
得a1=2,a2=1005,a3=1003,a4=-2,a5=-1005,a6=-1003S6=0,
且数列{an}是以6为周期的周期数列,
所以,S6n=0,
所以 S2009=S5=a3=1003--(3分)
(2)当p=0时,a1=a2=0,an+1=-2an2+2an=0,
即{an}是周期数列--(5分)
当p≠0,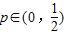 时,
时,
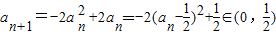
由已知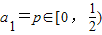 ,
,
且an+1=-2an2+2an,
可得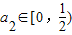 ,
,
依此类推可得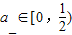 (n∈N*)
(n∈N*)
所以 an+1-an=-2an2+an=an(1-2an)>0,所以an+1>an
即数列{an}是递增数列,非周期数列;--(8分)
(3)由(1)知,S2=a1+a2=a1+1005=1007,
所以a1=2,a2=1005,a3=1003,a4=-2,a5=-1005,a6=-1003,
且数列{an}是周期为6的周期数列,
所以(an)max=1005(n∈N*),(an)min=-1005,
且 a6n+1=2,a6n+2=1003,a6n+3=1005,a6n+4=-2,
a6n+5=-1005,a6n+6=-1003,--(9分)
而当n≥12时,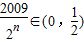 ,
,
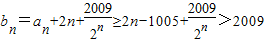 ,
,
即2n≥2009+1005=3014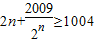 ,
,
得n≥1507,即 n≥1507时,
都有bn>2009;--(12分)
又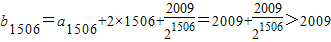
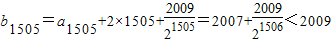 --(13分)
--(13分)
综上,存在最小的自然数n=1506,
对一切自然数m,当m≥n=1506,
都有bm>2009.--(14分)
点评:本题考查数列和不等式的综合运用,解题时要认真审题,仔细解答,注意挖掘题设中的隐条件,合理地进行等价转化.
(2)当p=0时,a1=a2=0,an+1=-2an2+2an=0,即{an}是周期数列,由此能推导出数列{an}是递增数列,非周期数列.
(3)由S2=a1+a2=a1+1005=1007,知a1=2,a2=1005,a3=1003,a4=-2,a5=-1005,a6=-1003,且数列{an}是周期为6的周期数列,由此能推导出存在最小的自然数n=1506,对一切自然数m,当m≥n=1506,都有bm>2009.
解答:解:(1)an+6=an+5-an-4=an+4-an+3-an-4
=-an+3=-an+2+an+1=-(an+1-an)+an+1=an,
得T=6
所以,数列{an}是以6为周期的周期数列,
周期为任意正整数--(2分)
又由
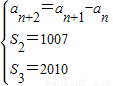 ,
,得a1=2,a2=1005,a3=1003,a4=-2,a5=-1005,a6=-1003S6=0,
且数列{an}是以6为周期的周期数列,
所以,S6n=0,
所以 S2009=S5=a3=1003--(3分)
(2)当p=0时,a1=a2=0,an+1=-2an2+2an=0,
即{an}是周期数列--(5分)
当p≠0,
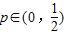 时,
时,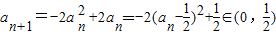
由已知
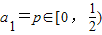 ,
,且an+1=-2an2+2an,
可得
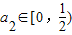 ,
,依此类推可得
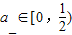 (n∈N*)
(n∈N*)所以 an+1-an=-2an2+an=an(1-2an)>0,所以an+1>an
即数列{an}是递增数列,非周期数列;--(8分)
(3)由(1)知,S2=a1+a2=a1+1005=1007,
所以a1=2,a2=1005,a3=1003,a4=-2,a5=-1005,a6=-1003,
且数列{an}是周期为6的周期数列,
所以(an)max=1005(n∈N*),(an)min=-1005,
且 a6n+1=2,a6n+2=1003,a6n+3=1005,a6n+4=-2,
a6n+5=-1005,a6n+6=-1003,--(9分)
而当n≥12时,
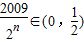 ,
,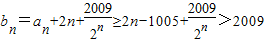 ,
,即2n≥2009+1005=3014
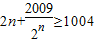 ,
,得n≥1507,即 n≥1507时,
都有bn>2009;--(12分)
又
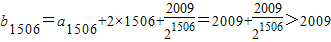
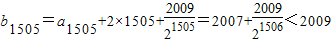 --(13分)
--(13分)综上,存在最小的自然数n=1506,
对一切自然数m,当m≥n=1506,
都有bm>2009.--(14分)
点评:本题考查数列和不等式的综合运用,解题时要认真审题,仔细解答,注意挖掘题设中的隐条件,合理地进行等价转化.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
对于数列{an},若满足a1,
,
,…,
,…是首项为1,公比为2的等比数列,则a100等于( )
| a2 |
| a1 |
| a3 |
| a2 |
| an |
| an-1 |
| A、2100 |
| B、299 |
| C、25050 |
| D、24950 |