网址:http://m.1010jiajiao.com/timu_id_34331[举报]
一.1.B 2.B 3.A 4.B 5.A 6.D 7.C 8.A 9.A 10.C
二.11.5
12.36
13. 14.
14. 
15. 适合① ②
②
 的不等式如:
的不等式如: ,
,  或其它曲线型只要适合即可
或其它曲线型只要适合即可
三.16.解: (1)



∴ 即AB边的长度为2.
…………… …………5分
即AB边的长度为2.
…………… …………5分
(2)由已知及(1)有:

∴ ……………8分
……………8分
由正弦定理得:  ……………10分
……………10分
∴ =
= …………12分
…………12分
17.解: ①依题意可设 ………1分
………1分
则
对n=1,2,3,……都成立 ………3分

∴ 又 解得
解得

∴ ………6分
………6分
②∵
 …………9分
…………9分
∴ +
+  +
+ +…+
+…+
 ……12分
……12分
18.解:(Ⅰ)依题意,记“甲投一次命中”为事件A,“乙投一次命中”为事件B,
则 …………3分
…………3分
∵“甲、乙两人各投球一次,都没有命中”的事件为
 …………5分
…………5分
(Ⅱ)∵甲、乙两人在罚球线各投球二次时,
甲命中1次,乙命中0次的概率为 …………7分
…………7分
甲命中2次,乙命中0次的概率为 …………9分
…………9分
甲命中2次,乙命中1次”的概率为 …………11分
…………11分
故甲、乙两人在罚球线各投球两次,甲投球命中的次数比乙投球命中的次数多的
概率为P= …………12分
…………12分
 19.解法1:取BE的中点O,连OC.
19.解法1:取BE的中点O,连OC.
∵BC=CE, ∴OC⊥BE.又AB⊥平面BCE.
以O为原点建立空间直角坐标系O-xyz如图,
则由已知条件有: ,
, ,
,

 ,
, ……4分
……4分
设平面ADE的法向量为n= ,
,
则由n?



及n?



可取n
 ……6分
……6分
又AB⊥平面BCE. ∴AB⊥OC.OC⊥平面ABE
∴平面ABE的法向量可取为m= .
.
∵n?m
 ?
? =0,
=0,
∴n⊥m∴平面ADE⊥平面ABE. ……8分
⑵点C到平面ADE的距离为 ……12分
……12分
解法2:取BE的中点O,AE的中点F,连OC,OF,CD.则


 ∵AB⊥平面BCE,CD⊥平面BCE, AB=2CD
∵AB⊥平面BCE,CD⊥平面BCE, AB=2CD
∴CD 
 ,
,
 CD∴
CD∴ ∥ FD ……3分
∥ FD ……3分
∵BC=CE, ∴OC⊥BE.又AB⊥平面BCE.
∴OC⊥平面ABE. ∴FD⊥平面ABE.
从而平面ADE.⊥平面ABE. ……6分
②∵CD 
 ,延长AD, BC交于T
,延长AD, BC交于T
则C为BT的中点.
点C到平面ADE的距离等于点B到平面ADE的距离的 .……8分
.……8分
过B作BH⊥AE,垂足为H。∵平面ADE.⊥平面ABE。∴BH⊥平面BDE.
由已知有AB⊥BE.
BE= ,AB= 2, ∴BH=
,AB= 2, ∴BH= ,
,
从而点C到平面ADE的距离为 ……………… ……………12分
……………… ……………12分
或 ∥ FD, 点C到平面ADE的距离等于点O到平面ADE的距离为
∥ FD, 点C到平面ADE的距离等于点O到平面ADE的距离为 .
.
或取A B的中点M。易证 ∥ DA。点C到平面ADE的距离等于点M到平面ADE的距离为
∥ DA。点C到平面ADE的距离等于点M到平面ADE的距离为 .
.
20. 解:
(I)设O为原点,则
 =2
=2 ,
,
 =2
=2 。
。
而
 =
= ,得
,得 =
=
 ,
,
于是O、P、Q三点共线。 ……………2分
因为 所以PF∥QF/,且
所以PF∥QF/,且  ,……………3分
,……………3分
得



 ,
,
∴ ∴
∴ ……………5分
……………5分
因此椭圆的离心率为 双曲线的离心率为
双曲线的离心率为 ……………7分
……………7分
(II)设 、
、 ,
,
点P在双曲线 的上,有
的上,有 。
。
则 .
.
所以 。 ①…………9分
。 ①…………9分
又由点Q在椭圆 上,有
上,有 。
。
同理可得 ②
……………10分
②
……………10分
∵O、P、Q三点共线。∴ 。
。
由①、②得 。
……………13分
。
……………13分
21. 解:(I)
 ……………1分
……………1分
由已知有: ∴
∴ ,∴
,∴ ……………3分
……………3分
从而

令 =0得:x1=1,x2=
=0得:x1=1,x2= . ∵
. ∵ ∴x2
∴x2
当x变化时, 、f(x)的变化情况如下表:
、f(x)的变化情况如下表:
x




+
-
+

增函数
减函数
增函数
从上表可知: 在
在 ,
, 上是增函数;
上是增函数;
在 ,上是减函数 ……………6分
,上是减函数 ……………6分
(II)∵m>0,∴m+1>1. 由(I)知:
①当0<m<1时, . 则最小值为
. 则最小值为 得:
得: ……8分
……8分
此时 .从而
.从而
∴最大值为 得
得
此时 适合. ……10分
适合. ……10分
②当m 1时,
1时,  在闭区间
在闭区间 上是增函数.
上是增函数.
∴最小值为
 ⑴
⑴
最大值为
 =0. ⑵………12分
=0. ⑵………12分
由⑵得: ⑶
⑶
⑶代入⑴得: .即
.即
又m 1,
1,  ∴
∴ 从而
从而
∴此时的a,m不存在
综上知:
 ,
, .
………14分
.
………14分
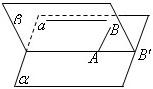 13、求证:若一直线与一个平面平行,则过平面内的一点且与这条直线平行的直线必在此平面内.
13、求证:若一直线与一个平面平行,则过平面内的一点且与这条直线平行的直线必在此平面内.