题目内容
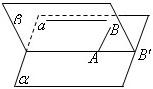13、求证：若一直线与一个平面平行，则过平面内的一点且与这条直线平行的直线必在此平面内．分析：先把题目转化为数学语言，并画出图形，设AB∥a，再由线面平行的性质定理证明线线平行，再得两条线重合．
解答：证明：已知：a∥α，
求证：过平面α内的一点且与a平行的直线必在α内．
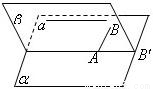
证明：如图，设A∈α，AB∥a．
∵AB∥a，∴它们确定一个平面β，
设α∩β=AB′，∵a∥α，∴a∥AB′，
在平面β内，过点A存在AB∥a，AB′∥a，
∴AB与AB′重合，即AB?α．
求证：过平面α内的一点且与a平行的直线必在α内．
证明：如图，设A∈α，AB∥a．
∵AB∥a，∴它们确定一个平面β，
设α∩β=AB′，∵a∥α，∴a∥AB′，
在平面β内，过点A存在AB∥a，AB′∥a，
∴AB与AB′重合，即AB?α．
点评：本题考查了线面平行的性质定理，用统一法证明；还考查了空间想象能力和逻辑思维能力．
练习册系列答案
阅读快车系列答案
相关题目
