题目内容
求证:对于任意不小于3的自然数,| 2n-1 |
| 2n+1 |
| n |
| n+1 |
分析:首先分析题目求任意不小于3的自然数都满足
>
,考虑到用数学归纳法去证明问题,首先验证当n=3时成立,再假设n=k成立去验证n=k+1是否成立,即可得证.
| 2n-1 |
| 2n+1 |
| n |
| n+1 |
解答:证明:要证
>
,只要证2n>2n+1 (n≥3)即可.
(1)当n=3时,23=8,2×3+1=7,不等式2n>2n+1成立.
(2)假设n=k(k≥3,且k∈N*)时,不等式成立,即2k>2k+1,
则2k+1=2•2k>2(2k+1)=4k+2=2(k+1)+2k>2(k+1)+1,
即2k+1>2(k+1)+1.
综合(1)、(2)可知,对于任意不小于3的自然数大于号恒成立.
即得证.
| 2n-1 |
| 2n+1 |
| n |
| n+1 |
(1)当n=3时,23=8,2×3+1=7,不等式2n>2n+1成立.
(2)假设n=k(k≥3,且k∈N*)时,不等式成立,即2k>2k+1,
则2k+1=2•2k>2(2k+1)=4k+2=2(k+1)+2k>2(k+1)+1,
即2k+1>2(k+1)+1.
综合(1)、(2)可知,对于任意不小于3的自然数大于号恒成立.
即得证.
点评:此题主要考查不等式的证明问题,其中涉及到数学归纳法的应用问题.数学归纳法在证明题中应用广泛,需要理解记忆.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
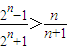 .
.