摘要：Dn=d1+d2+--+dn=2[1+()+()+()+--+()]
网址：http://m.1010jiajiao.com/timu_id_329102[举报]
(1)设函数g(x)＝
(x∈R)，且数列{cn}满足c1＝1，cn＝g(cn－1)(n∈N，n＞1)；求数列{cn}的通项公式．
(2)设等差数列{an}、{bn}的前n项和分别为Sn和Tn，且
，
，S2＝6；求常数A的值及{an}的通项公式．
(3)若
，其中an、cn即为(1)、(2)中的数列{an}、{cn}的第n项，试求d1＋d2＋…＋dn．
(1)设函数g(x)＝
(x∈R)，且数列{cn}满足c1＝1，cn＝g(cn－1)(n∈N，n＞1)；求数列{cn}的通项公式．
(2)设等差数列{an}、{bn}的前n项和分别为Sn和Tn，且
，
，S2＝6；求常数A的值及{an}的通项公式．
(3)若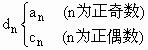
，其中an、cn即为(1)、(2)中的数列{an}、{cn}的第n项，试求d1＋d2＋…＋dn．
已知分别以d1和d2为公差的等差数列{an}和{bn}满足a1＝18，b14＝36．
(1)若d1＝18，且存在正整数m，使得
＝bm+14－45，求证：d2＞108；
(2)若ak＝bk＝0，且数列a1，a2，…，ak，bk+1，bk+2，…，b14的前n项和Sn满足S14＝2Sk，求数列{an}和{bn}的通项公式；
(3)在(2)的条件下，令cn＝
，dn＝
，问不等式cndn＋1≤cn＋dn是否对n∈N+恒成立？请说明理由．
有n个首项都是1的等差数列，设第m个数列的第k项为amk（m，k=1，2，3，…，n，n≥3），公差为dm，并且a1n，a2n，a3n，…，ann成等差数列．
（Ⅰ）证明dm=p1d1+p2d2（3≤m≤n，p1，p2是m的多项式），并求p1+p2的值；
（Ⅱ）当d1=1，d2=3时，将数列dm分组如下：（d1），（d2，d3，d4），（d5，d6，d7，d8，d9），…（每组数的个数构成等差数列）．设前m组中所有数之和为（cm）4（cm＞0），求数列{2cmdm}的前n项和Sn．
（Ⅲ）设N是不超过20的正整数，当n＞N时，对于（Ⅱ）中的Sn，求使得不等式
(Sn-6)＞dn成立的所有N的值．
查看习题详情和答案>>
（Ⅰ）证明dm=p1d1+p2d2（3≤m≤n，p1，p2是m的多项式），并求p1+p2的值；
（Ⅱ）当d1=1，d2=3时，将数列dm分组如下：（d1），（d2，d3，d4），（d5，d6，d7，d8，d9），…（每组数的个数构成等差数列）．设前m组中所有数之和为（cm）4（cm＞0），求数列{2cmdm}的前n项和Sn．
（Ⅲ）设N是不超过20的正整数，当n＞N时，对于（Ⅱ）中的Sn，求使得不等式
| 1 | 50 |
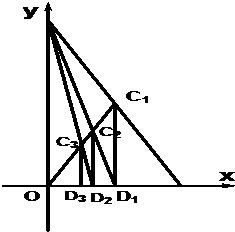如图，已知A（1，0），B（0，2），C1为AB的中点，O为坐标原点，过C1作C1D1⊥OA于D1点，连接BD1交OC1于C2点，过C2作C2D2⊥OA于D2点，连接BD2交OC1于C3点，过C3作C3D3⊥OA于D3点，如此继续，依次得到D1，D2，D3…Dn（n∈N*），记Dn的坐标为（an，0）．