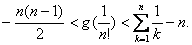题目内容
(1)设函数g(x)=![]() (x∈R),且数列{cn}满足c1=1,cn=g(cn-1)(n∈N,n>1);求数列{cn}的通项公式.
(x∈R),且数列{cn}满足c1=1,cn=g(cn-1)(n∈N,n>1);求数列{cn}的通项公式.
(2)设等差数列{an}、{bn}的前n项和分别为Sn和Tn,且![]() ,
,![]() ,S2=6;求常数A的值及{an}的通项公式.
,S2=6;求常数A的值及{an}的通项公式.
(3)若 ,其中an、cn即为(1)、(2)中的数列{an}、{cn}的第n项,试求d1+d2+…+dn.
,其中an、cn即为(1)、(2)中的数列{an}、{cn}的第n项,试求d1+d2+…+dn.
答案:
解析:
解析:
|
解:(1)由题意: ∴数列 ∴ (2)∵由等差数列 ∴由 ∴ ∴ ∴可设 当 当n≥2时, 综上得: (3)当 当 |

练习册系列答案
相关题目
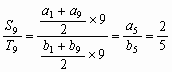 ,∵
,∵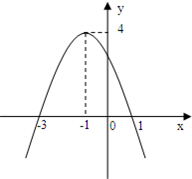 如图是一个二次函数y=f(x)的图象
如图是一个二次函数y=f(x)的图象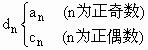 ,其中an、cn即为(1)、(2)中的数列{an}、{cn}的第n项,试求d1+d2+…+dn.
,其中an、cn即为(1)、(2)中的数列{an}、{cn}的第n项,试求d1+d2+…+dn.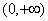 的函数
的函数 , 其中e=2.71828……是自然对数的底数,
, 其中e=2.71828……是自然对数的底数, 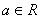 .
.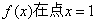 处连续, 求a的值;
处连续, 求a的值;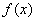 为(0, 1)上的单调函数, 求实数a的取值范围, 并判断此时函数
为(0, 1)上的单调函数, 求实数a的取值范围, 并判断此时函数 )上是否为单调函数;
)上是否为单调函数; 时, 有
时, 有