题目内容
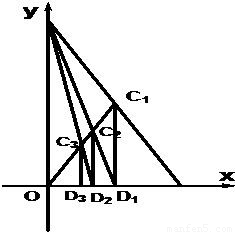
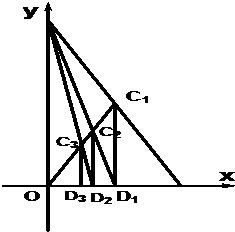 如图,已知A(1,0),B(0,2),C1为AB的中点,O为坐标原点,过C1作C1D1⊥OA于D1点,连接BD1交OC1于C2点,过C2作C2D2⊥OA于D2点,连接BD2交OC1于C3点,过C3作C3D3⊥OA于D3点,如此继续,依次得到D1,D2,D3…Dn(n∈N*),记Dn的坐标为(an,0).
如图,已知A(1,0),B(0,2),C1为AB的中点,O为坐标原点,过C1作C1D1⊥OA于D1点,连接BD1交OC1于C2点,过C2作C2D2⊥OA于D2点,连接BD2交OC1于C3点,过C3作C3D3⊥OA于D3点,如此继续,依次得到D1,D2,D3…Dn(n∈N*),记Dn的坐标为(an,0).(1)求a1,a2的值;
(2)求an与an+1的关系式,并求出an的表达式;
(3)设△OCnDn的面积为bn,数列{bn}的前n项和为Sn,证明:Sn<
| 3 | 4 |
分析:(1)由题意知直线BD1的方程:
+
=1,直线OC1的方程:y=2x,由此可解得C2的横坐标为a2=
.
(2)设Dn(an,0),由题意知直线BDn的方程为
+
=1,联立OC1:y=2x,可解得x=an+1=
,由引可知an=
.
(3)由题意知
=
=(
)2=(
)2=4an2,由此可知Sn=b1+b2+b3+bn=
+
+
++
<
+(
-
)+(
-
)+(
-
)=
-
<
.
| x | ||
|
| y |
| 2 |
| 1 |
| 3 |
(2)设Dn(an,0),由题意知直线BDn的方程为
| x |
| an |
| y |
| 2 |
| an |
| an+1 |
| 1 |
| n+1 |
(3)由题意知
| S△OCnDn |
| S△OC1D1 |
| bn |
| b1 |
| ODn |
| OD1 |
| an |
| a1 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| (n+1)2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
| 3 |
| 4 |
| 1 |
| n+1 |
| 3 |
| 4 |
解答:解(1)∵C1为AB中点,∴C1(
,1),D1(
,0),a1=
,
直线BD1的方程:
+
=1,直线OC1的方程:y=2x,
可解得C2的横坐标为a2=
(2分)
(2)设Dn(an,0),直线BDn的方程为
+
=1,联立OC1:y=2x,
可解得x=an+1=
,∴
=
+1(5分)
∴数列{
}是首项为2公差为1的等差数列,∴
=n+1,∴an=
(8分)
(3)b1=S△OC1D1=
∵△OCnDn~△OC1D1
∴
=
=(
)2=(
)2=4an2,
∴bn=an2=
(11分)
Sn=b1+b2+b3+bn=
+
+
++
<
+
+
++
=
+(
-
)+(
-
)+(
-
)
=
-
<
(14分)
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
直线BD1的方程:
| x | ||
|
| y |
| 2 |
可解得C2的横坐标为a2=
| 1 |
| 3 |
(2)设Dn(an,0),直线BDn的方程为
| x |
| an |
| y |
| 2 |
可解得x=an+1=
| an |
| an+1 |
| 1 |
| an+1 |
| 1 |
| an |
∴数列{
| 1 |
| an |
| 1 |
| an |
| 1 |
| n+1 |
(3)b1=S△OC1D1=
| 1 |
| 4 |
∴
| S△OCnDn |
| S△OC1D1 |
| bn |
| b1 |
| ODn |
| OD1 |
| an |
| a1 |
∴bn=an2=
| 1 |
| (n+1)2 |
Sn=b1+b2+b3+bn=
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| (n+1)2 |
| 1 |
| 22 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
=
| 3 |
| 4 |
| 1 |
| n+1 |
| 3 |
| 4 |
点评:本题综合考查数列的性质的应用,解题时要认真分析,仔细求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知A(-2,0),B(2,0),等腰梯形ABCD满足|AB|=-2|CD|,E为AC上一点,且
如图,已知A(-2,0),B(2,0),等腰梯形ABCD满足|AB|=-2|CD|,E为AC上一点,且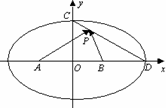
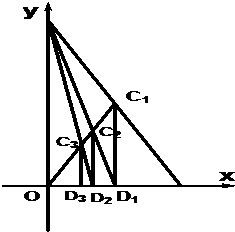 如图,已知A(1,0),B(0,2),C1为AB的中点,O为坐标原点,过C1作C1D1⊥OA于D1点,连接BD1交OC1于C2点,过C2作C2D2⊥OA于D2点,连接BD2交OC1于C3点,过C3作C3D3⊥OA于D3点,如此继续,依次得到D1,D2,D3…Dn(n∈N*),记Dn的坐标为(an,0).
如图,已知A(1,0),B(0,2),C1为AB的中点,O为坐标原点,过C1作C1D1⊥OA于D1点,连接BD1交OC1于C2点,过C2作C2D2⊥OA于D2点,连接BD2交OC1于C3点,过C3作C3D3⊥OA于D3点,如此继续,依次得到D1,D2,D3…Dn(n∈N*),记Dn的坐标为(an,0). .
.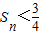 .
.