摘要:19.已知椭圆的离心率为.过右顶点A的直线l与椭圆C相交于A.B两点.且. (1)求椭圆C和直线l的方程, (2)记曲线C在直线l下方的部分与线段AB所围成的平面区域为D.若 曲线与D有公共点.试求实数m的最小值. [解](1)由离心率.得.即. ① ------2分 又点在椭圆上.即. ② ------4分 解 ①②得. 故所求椭圆方程为. -------6分 由得直线l的方程为. ---8分 (2)曲线. 即圆.其圆心坐标为.半径.表示圆心在直线 上.半径为的动圆. ------- 10分 由于要求实数m的最小值.由图可知.只须考虑的情形. 设与直线l相切于点T.则由.得.------- 12分 当时.过点与直线l垂直的直线的方程为. 解方程组得. ------- 14分 因为区域D内的点的横坐标的最小值与最大值分别为. 所以切点.由图可知当过点B时.m取得最小值.即. 解得. ------- 16分 (说明:若不说理由.直接由圆过点B时.求得m的最小值.扣4分)
网址:http://m.1010jiajiao.com/timu_id_3206423[举报]
(本小题满分16分)
已知椭圆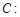
 的离心率为
的离心率为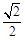 ,一条准线
,一条准线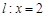 .
.
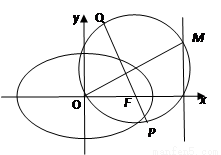
(1)求椭圆 的方程;
的方程;
(2)设O为坐标原点, 是
是 上的点,
上的点, 为椭圆
为椭圆 的右焦点,过点F作OM的垂线与以OM为直径的圆
的右焦点,过点F作OM的垂线与以OM为直径的圆 交于
交于 两点.
两点.
①若 ,求圆
,求圆 的方程;
的方程;
②若 是l上的动点,求证:点
是l上的动点,求证:点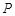 在定圆上,并求该定圆的方程.
在定圆上,并求该定圆的方程.
查看习题详情和答案>>
(本小题满分16分)
已知F是椭圆 :
: =1的右焦点,点P是椭圆
=1的右焦点,点P是椭圆 上的动点,点Q是圆
上的动点,点Q是圆 :
: +
+ =
= 上的动点.
上的动点.
(1)试判断以PF为直径的圆与圆 的位置关系;
的位置关系;
(2)在x轴上能否找到一定点M,使得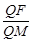 =e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.
=e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.
查看习题详情和答案>>
(本小题满分16分)已知椭圆 :
: 的离心率为
的离心率为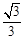 ,直线
,直线
 :
: 与椭圆
与椭圆 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)设椭圆 的左焦点为
的左焦点为 ,右焦点为
,右焦点为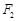 ,直线
,直线 过点
过点 且垂直与椭圆的长轴,动直线
且垂直与椭圆的长轴,动直线 垂直于直线
垂直于直线 于点
于点 ,线段
,线段 的垂直平分线交
的垂直平分线交 于点
于点 ,求点
,求点 的轨迹
的轨迹 的方程.
的方程.
查看习题详情和答案>>
 过点
过点 ,离心率为
,离心率为 ,圆
,圆 的圆心为坐标原点,直径为椭圆的短轴,圆
的圆心为坐标原点,直径为椭圆的短轴,圆 的方程为
的方程为 .过圆
.过圆 作圆
作圆 ,切点为
,切点为 .
. 与圆
与圆 ,当弦
,当弦 最大时,求直线
最大时,求直线 的最值.
的最值.
 的离心率为
的离心率为 ,一条准线
,一条准线 .
.
 的方程;
的方程; 是
是 上的点,
上的点, 为椭圆
为椭圆 交于
交于 两点.
两点. ,求圆
,求圆 在定圆上,并求该定圆的方程.
在定圆上,并求该定圆的方程.