摘要:(Ⅱ)若点是定直线上的任意一点.分别记直线的斜率为.试探求之间的关系.并给出证明.
网址:http://m.1010jiajiao.com/timu_id_312711[举报]
动点 到定点
到定点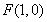 与到定直线,
与到定直线,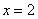 的距离之比为
的距离之比为 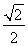 .
.
(1)求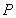 的轨迹方程;
的轨迹方程;
(2)过点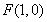 的直线
的直线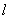 (与x轴不重合)与(1)中轨迹交于两点
(与x轴不重合)与(1)中轨迹交于两点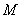 、
、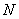 .探究是否存在一定点E(t,0),使得x轴上的任意一点(异于点E、F)到直线EM、EN的距离相等?若存在,求出t的值;若不存在,说明理由.
.探究是否存在一定点E(t,0),使得x轴上的任意一点(异于点E、F)到直线EM、EN的距离相等?若存在,求出t的值;若不存在,说明理由.
查看习题详情和答案>>
动点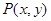 到定点
到定点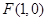 与到定直线,
与到定直线,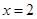 的距离之比为
的距离之比为 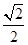 .
.
(1)求 的轨迹方程;
的轨迹方程;
(2)过点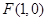 的直线
的直线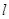 (与x轴不重合)与(1)中轨迹交于两点
(与x轴不重合)与(1)中轨迹交于两点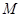 、
、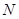 .探究是否存在一定点E(t,0),使得x轴上的任意一点(异于点E、F)到直线EM、EN的距离相等?若存在,求出t的值;若不存在,说明理由.
.探究是否存在一定点E(t,0),使得x轴上的任意一点(异于点E、F)到直线EM、EN的距离相等?若存在,求出t的值;若不存在,说明理由.
动点 到定点
到定点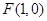 与到定直线,
与到定直线, 的距离之比为
的距离之比为  .
.
(1)求 的轨迹方程;
的轨迹方程;
(2)过点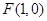 的直线
的直线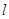 (与x轴不重合)与(1)中轨迹交于两点
(与x轴不重合)与(1)中轨迹交于两点 、
、 .探究是否存在一定点E(t,0),使得x轴上的任意一点(异于点E、F)到直线EM、EN的距离相等?若存在,求出t的值;若不存在,说明理由.
.探究是否存在一定点E(t,0),使得x轴上的任意一点(异于点E、F)到直线EM、EN的距离相等?若存在,求出t的值;若不存在,说明理由.
 到定点
到定点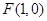 与到定直线,
与到定直线, 的距离之比为
的距离之比为  .
. (1)求
 的轨迹方程;
的轨迹方程;(2)过点
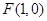 的直线
的直线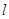 (与x轴不重合)与(1)中轨迹交于两点
(与x轴不重合)与(1)中轨迹交于两点 、
、 .探究是否存在一定点E(t,0),使得x轴上的任意一点(异于点E、F)到直线EM、EN的距离相等?若存在,求出t的值;若不存在,说明理由.
.探究是否存在一定点E(t,0),使得x轴上的任意一点(异于点E、F)到直线EM、EN的距离相等?若存在,求出t的值;若不存在,说明理由. 圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知椭圆C:
圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知椭圆C:| x2 |
| 4 |
(1)过椭圆C的右焦点作一条垂直于x轴的垂轴弦MN,求MN的长度;
(2)若点P是椭圆C上不与顶点重合的任意一点,MN是椭圆C的短轴,直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0)(如图),求xE?xF的值;
(3)在(2)的基础上,把上述椭圆C一般化为
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
 圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知点P(
圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知点P(x0,y0)、M(m,n)是圆锥曲线C上不与顶点重合的任意两点,MN是垂直于x轴的一条垂轴弦,直线MP,NP分别交x轴于点E(xE,0)和点F(xF,0).
(Ⅰ)试用x0,y0,m,n的代数式分别表示xE和xF;
(Ⅱ)已知“若点P(x0,y0)是圆C:x2+y2=R2上的任意一点(
x0•y0≠0),MN是垂直于x轴的垂轴弦,直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0),则xE•xF=R2”.类比这一结论,我们猜想:“若曲线C的方程为
| x2 |
| a2 |
| y2 |
| b2 |