题目内容
动点 到定点
到定点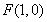 与到定直线,
与到定直线,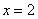 的距离之比为
的距离之比为 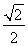 .
.
(1)求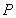 的轨迹方程;
的轨迹方程;
(2)过点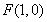 的直线
的直线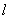 (与x轴不重合)与(1)中轨迹交于两点
(与x轴不重合)与(1)中轨迹交于两点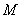 、
、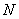 .探究是否存在一定点E(t,0),使得x轴上的任意一点(异于点E、F)到直线EM、EN的距离相等?若存在,求出t的值;若不存在,说明理由.
.探究是否存在一定点E(t,0),使得x轴上的任意一点(异于点E、F)到直线EM、EN的距离相等?若存在,求出t的值;若不存在,说明理由.
【答案】
(1)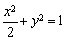 ;(2)2
;(2)2
【解析】
试题分析:(1)动点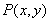 到定点
到定点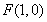 与到定直线,
与到定直线,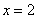 的距离之比为
的距离之比为 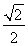 .根据两点的距离即点到直线的距离公式,即可求出结论.
.根据两点的距离即点到直线的距离公式,即可求出结论.
(2)根据题意假设直线方程联立椭圆方程消去y,得到一个关于x的二次方程,写出韦达定理得到M,N的坐标的关系式.因为题意要求x轴上的任意一点(异于点E、F)到直线EM、EN的距离相等,所以满足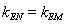 .结合韦达定理,即可得到结论.
.结合韦达定理,即可得到结论.
试题解析:(1)由题意得,  ,
,
化简得, 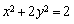 ,即
,即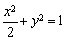 ,即点
,即点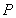 的轨迹方程
的轨迹方程
(2)若存在点E(t,0)满足题设条件.并设M(x1,y1)、N(x2,y2),
当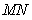 ⊥x轴时,由椭圆的对称性可知,x轴上的任意一点(异于点E、F)到直线EM、EN的距离相等
⊥x轴时,由椭圆的对称性可知,x轴上的任意一点(异于点E、F)到直线EM、EN的距离相等
当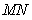 与x轴不垂直时,设直线l的方程为y=k(x-1)(k≠0).
与x轴不垂直时,设直线l的方程为y=k(x-1)(k≠0).
 ,得
,得 ,
,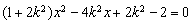
所以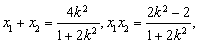
根据题意,x轴平分∠MEN,则直线ME、NE的倾斜角互补,即KME+KNE=0.
设E(t,0),则有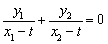 (当x1=t或x2=t时不合题意)
(当x1=t或x2=t时不合题意)
又k≠0,所以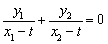 ,将y1=k(x1-1),y2=k(x2-1)代入上式,得
,将y1=k(x1-1),y2=k(x2-1)代入上式,得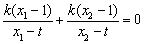
又k≠0,所以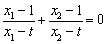 ,即
,即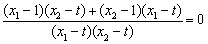 ,
,
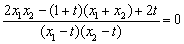 ,
,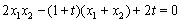 ,将
,将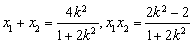 代入,解得t=2.
代入,解得t=2.
综上,存在定点E(2,0),使得x轴上的任意一点(异于点E、F)到直线EM、EN的距离相等.
考点:1.待定系数求椭圆的方程.2.直线与椭圆的位置关系.3.归纳转化的思想.4.运算能力.

练习册系列答案
相关题目
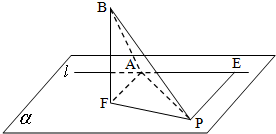 如图,平面α上定点F到定直线l的距离FA=2,曲线C是平面α上到定点F和到定直线l的距离相等的动点P的轨迹. 设FB⊥α,且FB=2.
如图,平面α上定点F到定直线l的距离FA=2,曲线C是平面α上到定点F和到定直线l的距离相等的动点P的轨迹. 设FB⊥α,且FB=2. (2006•海淀区二模)如图,平面内的定点F到定直线l的距离为2,定点E满足:|
(2006•海淀区二模)如图,平面内的定点F到定直线l的距离为2,定点E满足:|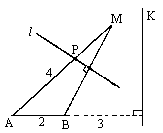
 上动点
上动点 到定点
到定点 与定直线
与定直线 的距离之比为常数
的距离之比为常数 .
. 引曲线C的弦AB恰好被点
引曲线C的弦AB恰好被点 平分,求弦AB所在的直线方程;
平分,求弦AB所在的直线方程; 为圆心作圆
为圆心作圆 ,设圆
,设圆 与点
与点 ,求
,求 的最小值,并求此时圆
的最小值,并求此时圆 作直线
作直线 的垂线,垂足为D.
的垂线,垂足为D. 代入坐标得到
代入坐标得到 ;,化简得
;,化简得
 ,, 不妨设
,, 不妨设 .
. .
.
 ,则
,则 ,
, ,故当
,故当 时,
时, 取得最小值为
取得最小值为 .
. ,故
,故 ,又点
,又点 在圆
在圆 上,代入圆的方程得到
上,代入圆的方程得到 .
. 