��Ŀ����
 Բ�����������������ɵ��߶γ�Ϊ�ң���Բ�����ϵ�һ���Ҵ�ֱ����Գ��ᣬ���ǽ����ҳ�֮Ϊ���ߵĴ����ң���֪��P��
Բ�����������������ɵ��߶γ�Ϊ�ң���Բ�����ϵ�һ���Ҵ�ֱ����Գ��ᣬ���ǽ����ҳ�֮Ϊ���ߵĴ����ң���֪��P��x0��y0����M��m��n����Բ����C�ϲ��붥���غϵ��������㣬MN�Ǵ�ֱ��x���һ�������ң�ֱ��MP��NP�ֱ�x���ڵ�E��xE��0���͵�F��xF��0����
��������x0��y0��m��n�Ĵ���ʽ�ֱ��ʾxE��xF��
������֪������P��x0��y0����ԲC��x2+y2=R2�ϵ�����һ�㣨
x0•y0��0����MN�Ǵ�ֱ��x��Ĵ����ң�ֱ��MP��NP�ֱ�x���ڵ�E��xE��0���͵�F��xF��0������xE•xF=R2���������һ���ۣ����Dz��룺��������C�ķ���Ϊ
| x2 |
| a2 |
| y2 |
| b2 |
�������������ֱ��lMP ���̣���y=0���ɵ�xE��ͬ�����ֱ��lNP ���̣���y=0�����xF��
�����ݣ��Ľ��ۣ�����M��P ����ԲC�ϣ������xE•xF��ֵ�����ɵõ����ۣ�
�����ݣ��Ľ��ۣ�����M��P ����ԲC�ϣ������xE•xF��ֵ�����ɵõ����ۣ�
������⣺��ΪMN�Ǵ�ֱ��x���һ�������ң�����N��m��-n����
��lMP��y-n=
(x-m) ����2�֣�
��y=0����xE=
����4�֣�
ͬ���ɵã�xF=
������6�֣�
����֤�����ɣ���֪��xE•xF=
��
=
������8�֣�
��M��P����ԲC��
+
=1(a��b��0)�ϣ�
��n2=b2(1-
)��
=b2(1-
)��������10�֣�
��xE•xF=
=
=a2����ֵ����
��xE•xF����MN�͵�Pλ���صĶ�ֵ������15�֣�
��lMP��y-n=
| y0-m |
| x0-m |
��y=0����xE=
| my0-nx0 |
| y0-n |
ͬ���ɵã�xF=
| my0+nx0 |
| y0+n |
����֤�����ɣ���֪��xE•xF=
| my0-nx0 |
| y0-n |
| my0+nx0 |
| y0+n |
| ||||
|
��M��P����ԲC��
| x2 |
| a2 |
| y2 |
| b2 |
��n2=b2(1-
| m2 |
| a2 |
| y | 2 0 |
| x02 |
| a2 |
��xE•xF=
| ||||
|
| ||||
|
��xE•xF����MN�͵�Pλ���صĶ�ֵ������15�֣�
���������⿼����Բ�Ķ��塢��Բ�ı����̣��Լ���Բ�ļ����ʵ�Ӧ�ã�����ѧ�������������������е��⣮

��ϰ��ϵ�д�
�����Ŀ
 Բ�����������������ɵ��߶γ�Ϊ�ң���Բ�����ϵ�һ���Ҵ�ֱ����Գ��ᣬ���ǽ����ҳ�֮Ϊ���ߵĴ����ң���֪��P��x0��y0����M��m��n����Բ����C�ϲ��붥���غϵ��������㣬MN�Ǵ�ֱ��x���һ�������ң�ֱ��MP��NP�ֱ�x���ڵ�E��xE��0���͵�F��xF��0����
Բ�����������������ɵ��߶γ�Ϊ�ң���Բ�����ϵ�һ���Ҵ�ֱ����Գ��ᣬ���ǽ����ҳ�֮Ϊ���ߵĴ����ң���֪��P��x0��y0����M��m��n����Բ����C�ϲ��붥���غϵ��������㣬MN�Ǵ�ֱ��x���һ�������ң�ֱ��MP��NP�ֱ�x���ڵ�E��xE��0���͵�F��xF��0���� Բ�����������������ɵ��߶γ�Ϊ�ң���Բ�����ϵ�һ���Ҵ�ֱ����Գ��ᣬ���ǽ����ҳ�֮Ϊ���ߵĴ����ң���֪��ԲC��
Բ�����������������ɵ��߶γ�Ϊ�ң���Բ�����ϵ�һ���Ҵ�ֱ����Գ��ᣬ���ǽ����ҳ�֮Ϊ���ߵĴ����ң���֪��ԲC��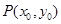 ��
�� ��Բ����C
��Բ����C �ϲ��붥���غϵ��������㣬
�ϲ��붥���غϵ��������㣬 �Ǵ�ֱ��
�Ǵ�ֱ�� ���һ�������ң�ֱ��
���һ�������ң�ֱ�� �ֱ�
�ֱ� �͵�
�͵� ��
��
 �Ĵ���ʽ�ֱ��ʾ
�Ĵ���ʽ�ֱ��ʾ ��
�� ��
�� ����ͼ������֤��
����ͼ������֤�� ����
���� λ���صĶ�ֵ��
λ���صĶ�ֵ�� ����Ƿ�����
����Ƿ����� ���������һ���ۣ����Dz��룺��������C�ķ���Ϊ
���������һ���ۣ����Dz��룺��������C�ķ���Ϊ ����ͼ������xE•xFҲ�����M��N��Pλ���صĶ�ֵ��������Ըò������֤����
����ͼ������xE•xFҲ�����M��N��Pλ���صĶ�ֵ��������Ըò������֤����