题目内容
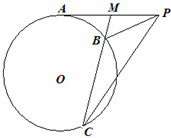
(1)自圆O外一点P引切线与圆切于点A,M为PA中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB.
(2)在平面直角坐标系xOy中,已知四边形ABCD的四个顶点A(0,1),B(2,1),C(2,3),D(0,2),经矩阵M=
表示的变换作用后,四边形ABCD变为四边形A1B1C1D1,问:四边形ABCD与四边形A1B1C1D1的面积是否相等?试证明你的结论.
(3)已知A是曲线ρ=12sinθ上的动点,B是曲线ρ=12cos(θ-
)上的动点,试求AB的最大值.
(4)设p是△ABC内的一点,x,y,z是p到三边a,b,c的距离,R是△ABC外接圆的半径,证明
+
+
≤
.
(2)在平面直角坐标系xOy中,已知四边形ABCD的四个顶点A(0,1),B(2,1),C(2,3),D(0,2),经矩阵M=
|
(3)已知A是曲线ρ=12sinθ上的动点,B是曲线ρ=12cos(θ-
| π |
| 6 |
(4)设p是△ABC内的一点,x,y,z是p到三边a,b,c的距离,R是△ABC外接圆的半径,证明
| x |
| y |
| z |
| 1 | ||
|
| a2+b2+c2 |

(1)证明:∵AM切圆于点A,∴AM2=MB•MC
又∵M为PA中点,AM=MP,∴MP2=MB•MC,∴
=
∵∠BMP=∠PMC,∴△BMP∽△PMC,∴∠MCP=∠MPB.
(2)四个顶点A(0,1),B(2,1),C(2,3),D(0,2),经矩阵M=
表示的变换作用后,四边形ABCD变为四边形A1B1C1D1顶点坐标为A1(0,1),B1(2,2k+1),C1(2,2k+3),D1(0,2),四边形A1B1C1D1仍为梯形,且上、下底及高都不变,故面积相等;
(3)曲线ρ=12sinθ化为直角坐标方程为 x2+(y-6)2=36,表示以(0,6)为圆心,以6为半径的圆.
曲线ρ=12cos(θ-
)化为直角坐标方程为 x2+y2=6
x+6y,即 (x-3
)2+(y-3)2=36,
表示以(3
,3 )为圆心,以6为半径的圆.
两圆的圆心距的平方为 (0-3
)2+(6-3)2 =36,故两圆相交,线段AB长的最大值为6+r+r′=18.
(4)连接P与三角形的三个顶点,分成的三个小三角形面积的和等于大三角形,即
(ax+by+cz)=S,∴ax+by+cz=2S=
∴
+
+
=
×
+
×
+
×
≤
×[(
)2+(
)2+(
)2]
=
×(
+
+
)=
×
=
≤
即
+
+
≤
又∵M为PA中点,AM=MP,∴MP2=MB•MC,∴
| PM |
| BM |
| CM |
| PM |
∵∠BMP=∠PMC,∴△BMP∽△PMC,∴∠MCP=∠MPB.
(2)四个顶点A(0,1),B(2,1),C(2,3),D(0,2),经矩阵M=
|
(3)曲线ρ=12sinθ化为直角坐标方程为 x2+(y-6)2=36,表示以(0,6)为圆心,以6为半径的圆.
曲线ρ=12cos(θ-
| π |
| 6 |
| 3 |
| 3 |
表示以(3
| 3 |
两圆的圆心距的平方为 (0-3
| 3 |
(4)连接P与三角形的三个顶点,分成的三个小三角形面积的和等于大三角形,即
| 1 |
| 2 |
| abc |
| 2R |
∴
| x |
| y |
| z |
| ax |
|
| by |
|
| cz |
|
≤
(
|
|
|
|
=
| ax+by+cz |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| abc |
| 2R |
| ab+bc+ac |
| abc |
| ab+bc+ac |
| 2R |
| 1 | ||
|
| a2+b2+c2 |
即
| x |
| y |
| z |
| 1 | ||
|
| a2+b2+c2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 (1)自圆O外一点P引切线与圆切于点A,M为PA中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB.
(1)自圆O外一点P引切线与圆切于点A,M为PA中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB. 表示的变换作用后,四边形ABCD变为四边形A1B1C1D1,问:四边形ABCD与四边形A1B1C1D1的面积是否相等?试证明你的结论.
表示的变换作用后,四边形ABCD变为四边形A1B1C1D1,问:四边形ABCD与四边形A1B1C1D1的面积是否相等?试证明你的结论. 上的动点,试求AB的最大值.
上的动点,试求AB的最大值. .
.
 表示的变换作用后,四边形ABCD变为四边形A1B1C1D1,问:四边形ABCD与四边形A1B1C1D1的面积是否相等?试证明你的结论.
表示的变换作用后,四边形ABCD变为四边形A1B1C1D1,问:四边形ABCD与四边形A1B1C1D1的面积是否相等?试证明你的结论.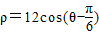 上的动点,试求AB的最大值.
上的动点,试求AB的最大值. .
.