题目内容
 如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,AC=2
如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,AC=2| 3 |
(Ⅰ)求证SA⊥SC;
(Ⅱ)在平面几何中,推导三角形内切圆的半径公式r=
| 2S |
| l |
①以内切圆的圆心O为顶点,将三角形ABC分割成三个小三角形:△OAB,△OAC,△OB
 C.
C.②设△ABC三边长分别为a,b,c.由S△ABC=S△OBC+S△OAC+S△OAB,
得S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2S |
| l |
类比上述方法,请给出四面体内切球半径的计算公式(不要求说明类比过程),并利用该公式求出三棱锥S-ABC内切球的半径.
分析:(I)过S作SO⊥AB,垂足为O,由已知中侧面SAB⊥底面ABC,结合面面垂直的性质可得OS⊥底面ABC.以O为坐标原点,OA为x轴,OS为z轴,建立空间直角坐标系,分别求出直线SA与SC的方向向量,代入向量的数量积公式,即可得到SA⊥SC;
(Ⅱ)根据平面内与面积相关的性质可类比为空间内与体积有关的性质,我们可以类比平面中r=
,得到r=
,连接球心与四个顶点,将大三棱锥分解为四个小三棱锥,然后根据四个小棱锥的体积和等于大棱锥的体积,即可证明结论.
(Ⅱ)根据平面内与面积相关的性质可类比为空间内与体积有关的性质,我们可以类比平面中r=
| 2S |
| l |
| 3V |
| S |
解答: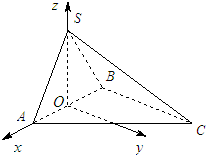 解:(Ⅰ)过S作SO⊥AB,垂足为O,
解:(Ⅰ)过S作SO⊥AB,垂足为O,
∵侧面SAB⊥底面ABC,∴OS⊥底面ABC.
∵SA=SB,∴O为AB中点.
以O为坐标原点,OA为x轴,OS为z轴,建立空间直角坐标系如图所示.
∵∠ASB=∠ABC=90°,AS=SB=2,AC=2
,
∴AB=2
,BC=2,OS=
,
∴A(
,0,0),C(-
,2,0),S(0,0,
).
∴
=(
,0,-
),
=(-
,2,-
).
则
•
=-2+0+2=0.
∴SA⊥SC.
(Ⅱ)三棱锥内切球的半径公式为r=
(其中V为三棱锥的体积,S为三棱锥的表面积).
在Rt△SAB中,SA=SB=2,∴S△SAB=2.
在Rt△ABC中,AB=2
,AC=2
,∴BC=2.∴S△ABC=2
.
在Rt△SAC中,SA=2,AC=2
,∴SC=2
.∴S△SAC=2
.B(-
,0,0),
=(0,2,0),
=(-
,0,-
),
∴
•
=0,则BC⊥SB.
在Rt△SBC中,SB=2,BC=2.∴S△SBC=2.
又VS-ABC=
S△ABC•SO=
.
∴r=
=
-1.
 解:(Ⅰ)过S作SO⊥AB,垂足为O,
解:(Ⅰ)过S作SO⊥AB,垂足为O,∵侧面SAB⊥底面ABC,∴OS⊥底面ABC.
∵SA=SB,∴O为AB中点.
以O为坐标原点,OA为x轴,OS为z轴,建立空间直角坐标系如图所示.
∵∠ASB=∠ABC=90°,AS=SB=2,AC=2
| 3 |
∴AB=2
| 2 |
| 2 |
∴A(
| 2 |
| 2 |
| 2 |
∴
| SA |
| 2 |
| 2 |
| SC |
| 2 |
| 2 |
则
| SA |
| SC |
∴SA⊥SC.
(Ⅱ)三棱锥内切球的半径公式为r=
| 3V |
| S |
(其中V为三棱锥的体积,S为三棱锥的表面积).
在Rt△SAB中,SA=SB=2,∴S△SAB=2.
在Rt△ABC中,AB=2
| 2 |
| 3 |
| 2 |
在Rt△SAC中,SA=2,AC=2
| 3 |
| 2 |
| 2 |
| 2 |
| BC |
| SB |
| 2 |
| 2 |
∴
| BC |
| SB |
在Rt△SBC中,SB=2,BC=2.∴S△SBC=2.
又VS-ABC=
| 1 |
| 3 |
| 4 |
| 3 |
∴r=
| 3V |
| S |
| 2 |
点评:本题考查的知识点是平面与平面垂直的性质,线线垂直的判定,类比推理,(1)的关键是建立空间坐标系,将线线垂直问题转化为向量垂直问题,(2)的关键是将大三棱锥分解为四个小三棱锥,根据四个小棱锥的体积和等于大棱锥的体积,得到结论.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC.
如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC. 如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( )
如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( ) 如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2
如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2 (2013•杭州模拟)如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是( )
(2013•杭州模拟)如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是( ) (2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )
(2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )