网址：http://m.1010jiajiao.com/timu_id_30950[举报]
一、选择题（每小题5分，共60分）
1－12BDCBC CCDBA AC
二、填空题（每题4分，共16分）
13、
14、
15、1 16、15
三、解答题（共74分）
17、（本小题满分12分）
（1）
函数
的最小正周期是
当
时，即
时，函数有最大值1。
（2）由
，得
当
时，取
得，函数的单调递减区间是
（3）
18、（本小题满分12分）
（1）由题意知：
且
，∴
＝1
∵
①，∴当 n≥2时, 
②
①－②得：
∴
∵
＞0，∴
，（n≥2且
）
∴
是以＝1为首项，d＝1为公差的等差数列
∴＝n
（2）
∴
是以
为首项，
为公比的等比数列
∴
，∴
，
∴
①
∴
②
①－②得
∴
19、（本小题满分12分）
（1）当
时，
在
上是增函数
∴在
上是增函数
∴当
时，
（2）
在上恒成立
∴
在上恒成立
∴
在上恒成立
在上是减函数，
∴当
时，
∴
，
∴所求实数a的取值范围为
20、（本小题满分12分）
由
此时
∴
又
，∴
，∴
∴实数a不存在
21、（本小题满分12分）
（1）若方程表示圆，则
，∴
（2）设M、N的坐标分别为
、
由
，得
又
，∴
，∴
①
由
，得
∴
代入①得
，
∴
（3）设MN为直径的圆的方程为
，
即
又
∴所求圆的方程为
22、（本小题满分14分）
（1）当
时，
设x为其不动点，则
，即
∴
或2，即的不动点是－1，2
（2）由
得
由题意知，此方程恒有两个相异的实根
∴
对任意的
恒成立
∴
，∴
（3）设
，则直线AB的斜率
，∴
由（2）知AB中点M的坐标为
又∵M在线段AB的垂直平分线
上，∴
∴
（当且仅当
时取等号）
∴实数b的取值范围为
（本小题满分14分） 对于函数f（x），
若存在x0∈R，使f（x0）=x0成立， 则称x0为f（x）的不动点. 已知函数f（x）=ax2+（b+1）x+b－1（a≠0）
（1）当a=1，b=－2时，求f（x）的不动点；
（2）若对于任意实数b，函数f（x）恒有两个相异的不动点，求a的取值范围
（本小题满分14分）已知函数f(x)=aex，g(x)= lna-ln(x +1)（其中a为常数，e为自然对数底），函数y =f(x)在A(0，a)处的切线与y =g(x)在B(0，lna)处的切线互相垂直.
(Ⅰ) 求f(x) ，g(x)的解析式；
(Ⅱ) 求证：对任意n ÎN*， f(n)+g(n)>2n；
(Ⅲ) 设y =g(x-1)的图象为C1，h(x)=-x2+bx的图象为C2，若C1与C2相交于P、Q，过PQ中点垂直于x轴的直线分别交C1、C2于M、N，问是否存在实数b，使得C1在M处的切线与C2在N处的切线平行？说明你的理由.
查看习题详情和答案>>（本小题满分14分）已知函数f(x)=aex，g(x)= lna-ln(x +1)（其中a为常数，e为自然对数底），函数y =f(x)在A(0，a)处的切线与y =g(x)在B(0，lna)处的切线互相垂直.
(Ⅰ) 求f(x) ，g(x)的解析式；
(Ⅱ) 求证：对任意n ÎN*， f(n)+g(n)>2n；
(Ⅲ) 设y =g(x-1)的图象为C1，h(x)=-x2+bx的图象为C2，若C1与C2相交于P、Q，过PQ中点垂直于x轴的直线分别交C1、C2于M、N，问是否存在实数b，使得C1在M处的切线与C2在N处的切线平行？说明你的理由.
查看习题详情和答案>>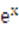
－kx，.
（2）若k>0，且对于任意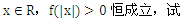
确定实数k的取值范围；
（
）。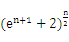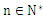