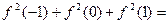题目内容
(本小题满分14分)已知函数f(x)满足对任意实数x,y都有f(x+y)=f(x)+f(y)+xy+1,且f(-2)=-2.
(1)求f(1)的值;
(2)证明:对一切大于1的正整数t,恒有f(t)>t;
(3)试求满足f(t)=t的整数的个数,并说明理由.
(1)求f(1)的值;
(2)证明:对一切大于1的正整数t,恒有f(t)>t;
(3)试求满足f(t)=t的整数的个数,并说明理由.
(1) f(1)=1;(2)略;(3)1和-2
(1)解:令x=y=0,得f(0)=-1.
令x=y=-1,因f(-2)=-2,所以f(-1)=-2.
令x=1,y=-1,得f(0)=f(1)+f(-1),
所以f(1)="1. " 4分
(2)证明:令x=1,得f(y+1)-f(y)=y+2,
故当y∈N时,有f(y+1)-f(y)>0.
由f(y+1)>f(y),f(1)=1可知,对一切正整数y都有f(y)>0.
当y∈N时,f(y+1)=f(y)+y+2=f(y)+1+y+1>y+1.
故对一切大于1的正整数,恒有f(t)>t. 9分
(3)解:由f(y+1)-f(y)=y+2及(1)可知f(-3)=-1,f(-4)=1.
下面证明t≤-4时,f(t)>t.
∵t≤-4,∴-(t+2)≥2>0.
∵f(t)-f(t+1)=-(t+2)>0,∴f(-5)-f(-4)>0,
同理可得f(-6)-f(-5)>0,f(t+1)-f(t+2)>0,f(t)-f(t+1)>0.
将各不等式相加得f(t)>f(-4)=1>-4.
∵t≤-4,∴f(t)>t.
综上所述,满足条件的整数只有两个:1和-2.………… 14分
令x=y=-1,因f(-2)=-2,所以f(-1)=-2.
令x=1,y=-1,得f(0)=f(1)+f(-1),
所以f(1)="1. " 4分
(2)证明:令x=1,得f(y+1)-f(y)=y+2,
故当y∈N时,有f(y+1)-f(y)>0.
由f(y+1)>f(y),f(1)=1可知,对一切正整数y都有f(y)>0.
当y∈N时,f(y+1)=f(y)+y+2=f(y)+1+y+1>y+1.
故对一切大于1的正整数,恒有f(t)>t. 9分
(3)解:由f(y+1)-f(y)=y+2及(1)可知f(-3)=-1,f(-4)=1.
下面证明t≤-4时,f(t)>t.
∵t≤-4,∴-(t+2)≥2>0.
∵f(t)-f(t+1)=-(t+2)>0,∴f(-5)-f(-4)>0,
同理可得f(-6)-f(-5)>0,f(t+1)-f(t+2)>0,f(t)-f(t+1)>0.
将各不等式相加得f(t)>f(-4)=1>-4.
∵t≤-4,∴f(t)>t.
综上所述,满足条件的整数只有两个:1和-2.………… 14分

练习册系列答案
相关题目

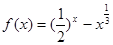 ,那么在下列区间中含有函数
,那么在下列区间中含有函数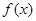 零点的是
零点的是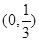



 和
和 ,它们的交点是P(
,它们的交点是P( ),若曲线C的方程为
),若曲线C的方程为
 +
+
 ="0" (
="0" ( 0时曲线C经过点P
0时曲线C经过点P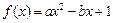 .
.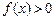 的解集是
的解集是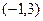 ,求实数
,求实数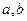 的值;
的值;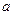 为整数,
为整数,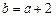 ,且函数
,且函数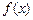 在
在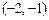 上恰有一个零点,求
上恰有一个零点,求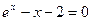 的一个零点所在的区间为
的一个零点所在的区间为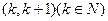 ,则k的值为 。
,则k的值为 。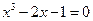 的一个近似解时,已经将一根锁定在区间(1,
的一个近似解时,已经将一根锁定在区间(1,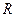 上的函数
上的函数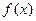 满足:①对任意
满足:①对任意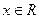 ,都有
,都有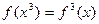 ;②对任意的
;②对任意的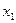 ,
,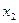
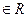 ,
,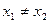 ,都有
,都有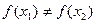 .那么
.那么