题目内容
(本小题满分14分) 对于函数f(x), 若存在x0∈R,使f(x0)=x0成立, 则称x0为f(x)的不动点. 已知函数f(x)=ax2+(b+1)x+b-1(a≠0)
若存在x0∈R,使f(x0)=x0成立, 则称x0为f(x)的不动点. 已知函数f(x)=ax2+(b+1)x+b-1(a≠0)
(1)当a=1,b=-2时,求f(x)的不动点;
(2)若对于任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围
解:(1)当a=1,b=-2时,f(x)=x2-x-3=x x2-2x-3=0
x2-2x-3=0 (x-3)(x+1)=0
(x-3)(x+1)=0 x=3或x=-1,
x=3或x=-1,
∴f(x)的不动点为x=3或x=-1. -----------------------------5
(2)对于任意实数b,f(x)恒有两个相异不动点 对任意实数b,ax2+(b+1)x+b-1=x恒有两个不等实根
对任意实数b,ax2+(b+1)x+b-1=x恒有两个不等实根
即ax2+bx+b-1=0恒有两个不等实根 对任意实数b,Δ=b2-4a(b-1)>0恒成立-------------------5
对任意实数b,Δ=b2-4a(b-1)>0恒成立-------------------5 对任意实数b,b2-4ab+4a>0恒成立
对任意实数b,b2-4ab+4a>0恒成立 Δ′=16a2-16a<0
Δ′=16a2-16a<0 a(a-1)<0
a(a-1)<0 0<a<1. ------------------------------4
0<a<1. ------------------------------4
解析

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
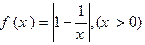
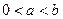 ,且
,且 时,求证:
时,求证: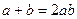
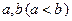 ,使得函数
,使得函数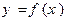 的定义域、值域都是
的定义域、值域都是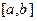 ?若存在,则求出
?若存在,则求出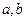 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。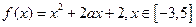 .
. 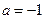 时,求函数f(x)
时,求函数f(x) 的最大值和最小值;
的最大值和最小值;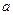 的取值范围,使
的取值范围,使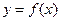 在区间
在区间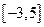 上是单调函数
上是单调函数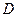 上的函数
上的函数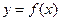
 满足条件:存在实数
满足条件:存在实数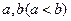 且
且

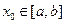 ,有
,有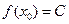 (
(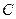 是常数);
是常数); ,当
,当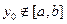 ,总有
,总有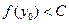 。
。 称为“平顶型”函数,称
称为“平顶型”函数,称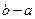 为“平顶宽度”。根据上述定义,解决下列问题:
为“平顶宽度”。根据上述定义,解决下列问题: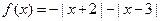 是否为“平顶型”函
是否为“平顶型”函 数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。
数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。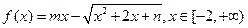 是“平顶型”函数,求出
是“平顶型”函数,求出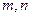 的值。
的值。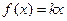 在
在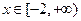 上有两个不相等的根,求实数
上有两个不相等的根,求实数 的取值范围。
的取值范围。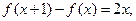 且f(0)=1.
且f(0)=1. 上,y= f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
上,y= f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围. 且每批均需付运费4元,储存购入的书桌一个月所付的保管费与每批购入书桌的总价值(不含运费)成正比,若每批购入4台,则该月需用去运费和保管费共52元,现在全月只有48元资金可以用于支付运费和保管费.
且每批均需付运费4元,储存购入的书桌一个月所付的保管费与每批购入书桌的总价值(不含运费)成正比,若每批购入4台,则该月需用去运费和保管费共52元,现在全月只有48元资金可以用于支付运费和保管费.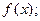
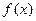 对一切实数x,y都有
对一切实数x,y都有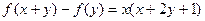 成立,且
成立,且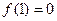 .
.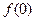 的值
的值 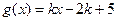 ,对任意的
,对任意的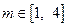 ,总存在
,总存在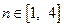 ,使得
,使得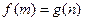 成立,求实数
成立,求实数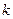 的取值范围
的取值范围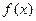 的定义域为
的定义域为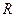 ,并满足(1)对于一切实数
,并满足(1)对于一切实数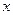 ,都有
,都有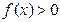 ;
;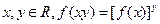 ; (3)
; (3)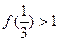 ;
;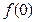 ;
;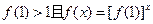 ;
;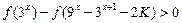 对任意的
对任意的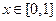 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。