摘要:综合①②得a的取值范围为a≤3.
网址:http://m.1010jiajiao.com/timu_id_29271[举报]
某市环保研究所对市中心每天环境污染情况进行调查研究后,发现一天中环境综合污染指数f(x)与时间x(小时)的关系为f(x)=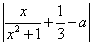 +2a,x∈[0,24],其中a与气象有关的参数,且a∈[0,
+2a,x∈[0,24],其中a与气象有关的参数,且a∈[0,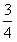 ],若用每天f(x)的最大值为当天的综合污染指数,并记作M(a)。
],若用每天f(x)的最大值为当天的综合污染指数,并记作M(a)。
(1)令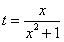 ,x∈[0,24],求t的取值范围;
,x∈[0,24],求t的取值范围;
(2)求函数M(a);
(3)市政府规定,每天的综合污染指数不得超过2,试问目前市中心的综合污染指数是多少?是否超标?
查看习题详情和答案>>
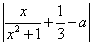 +2a,x∈[0,24],其中a与气象有关的参数,且a∈[0,
+2a,x∈[0,24],其中a与气象有关的参数,且a∈[0,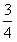 ],若用每天f(x)的最大值为当天的综合污染指数,并记作M(a)。
],若用每天f(x)的最大值为当天的综合污染指数,并记作M(a)。(1)令
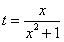 ,x∈[0,24],求t的取值范围;
,x∈[0,24],求t的取值范围;(2)求函数M(a);
(3)市政府规定,每天的综合污染指数不得超过2,试问目前市中心的综合污染指数是多少?是否超标?
某市环保研究所对市中心每天环境污染情况进行调查研究后,发现一天中环境综合污染指数f(x)与时间x(小时)的关系为![]() ,其中a是与气象有关的参数,且
,其中a是与气象有关的参数,且![]() ,若用每天f(x)的最大值为当天的综合污染指数,并记作M(a).
,若用每天f(x)的最大值为当天的综合污染指数,并记作M(a).
(1)令![]() ,求t的取值范围;
,求t的取值范围;
(2)求函数M(a);
(3)市政府规定,每天的综合污染指数不得超过2,试问目前市中心的综合污染是否超标?请说明理由.
市环境检测中心对化工工业园区每天环境污染情况进行调查研究后,发现一天中环境综合污染指数f(x)与时间x(小时)的关系为![]() ,其中a是与气象有关的参数,且
,其中a是与气象有关的参数,且![]() ,若记每天f(x)的最大值为当天的综合污染指数,并记作M(a).
,若记每天f(x)的最大值为当天的综合污染指数,并记作M(a).
(1)令![]() ,求t的取值范围;
,求t的取值范围;
(2)求函数M(a);
(3)根据环境要求的规定,每天的综合污染指数不得超过2,试问目前该工业园区的综合污染指数是多少?是否超标?
某地开发了一个旅游景点,第1年的游客约为100万人,第2年的游客约为120万人.某数学兴趣小组综合各种因素预测:①该景点每年的游客人数会逐年增加;②该景点每年的游客都达不到130万人.该兴趣小组想找一个函数y=f(x)来拟合该景点对外开放的第x(x≥1)年与当年的游客人数y(单位:万人)之间的关系.
(1)根据上述两点预测,请用数学语言描述函数y=f(x)所具有的性质;
(2)若f(x)=
+n,试确定m,n的值,并考察该函数是否符合上述两点预测;
(3)若f(x)=a•bx+c(b>0,b≠1),欲使得该函数符合上述两点预测,试确定b的取值范围.
查看习题详情和答案>>
(1)根据上述两点预测,请用数学语言描述函数y=f(x)所具有的性质;
(2)若f(x)=
| m | x |
(3)若f(x)=a•bx+c(b>0,b≠1),欲使得该函数符合上述两点预测,试确定b的取值范围.
某市为了对学生的数理(数学与物理)学习能力进行分析,从10000名学生中随机抽出100位学生的数理综合学习能力等级分数(6分制)作为样本,分数频数分布如下表:
(Ⅰ)如果以能力等级分数大于4分作为良好的标准,从样本中任意抽取2名学生,求恰有1名学生为良好的概率;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值(例如区间(1,2]的中点值为1.5)作为代表:
(ⅰ)据此,计算这100名学生数理学习能力等级分数的期望μ及标准差σ(精确到0.1);
(ⅱ) 若总体服从正态分布,以样本估计总体,估计该市这10000名学生中数理学习能力等级在(1.9,4.1)范围内的人数.
(Ⅲ)从这10000名学生中任意抽取5名同学,他们数学与物理单科学习能力等级分数如下表:

(ⅰ)请画出右上表数据的散点图;
(ⅱ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
=bx+a(附参考数据:
≈11.4)
查看习题详情和答案>>
| 等级得分 | (0,1] | (1,2] | (2,3] | (3,4] | (4,5] | (5,6] |
| 人数 | 3 | 17 | 30 | 30 | 17 | 3 |
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值(例如区间(1,2]的中点值为1.5)作为代表:
(ⅰ)据此,计算这100名学生数理学习能力等级分数的期望μ及标准差σ(精确到0.1);

(ⅱ) 若总体服从正态分布,以样本估计总体,估计该市这10000名学生中数理学习能力等级在(1.9,4.1)范围内的人数.
(Ⅲ)从这10000名学生中任意抽取5名同学,他们数学与物理单科学习能力等级分数如下表:

(ⅰ)请画出右上表数据的散点图;
(ⅱ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
 |
| y |
| 129 |