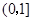题目内容
某市为了对学生的数理(数学与物理)学习能力进行分析,从10000名学生中随机抽出100位学生的数理综合学习能力等级分数(6分制)作为样本,分数频数分布如下表:
(Ⅰ)如果以能力等级分数大于4分作为良好的标准,从样本中任意抽取2名学生,求恰有1名学生为良好的概率;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值(例如区间(1,2]的中点值为1.5)作为代表:
(ⅰ)据此,计算这100名学生数理学习能力等级分数的期望μ及标准差σ(精确到0.1);
(ⅱ) 若总体服从正态分布,以样本估计总体,估计该市这10000名学生中数理学习能力等级在(1.9,4.1)范围内的人数.
(Ⅲ)从这10000名学生中任意抽取5名同学,他们数学与物理单科学习能力等级分数如下表:

(ⅰ)请画出右上表数据的散点图;
(ⅱ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
=bx+a(附参考数据:
≈11.4)
| 等级得分 | (0,1] | (1,2] | (2,3] | (3,4] | (4,5] | (5,6] |
| 人数 | 3 | 17 | 30 | 30 | 17 | 3 |
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值(例如区间(1,2]的中点值为1.5)作为代表:
(ⅰ)据此,计算这100名学生数理学习能力等级分数的期望μ及标准差σ(精确到0.1);

(ⅱ) 若总体服从正态分布,以样本估计总体,估计该市这10000名学生中数理学习能力等级在(1.9,4.1)范围内的人数.
(Ⅲ)从这10000名学生中任意抽取5名同学,他们数学与物理单科学习能力等级分数如下表:

(ⅰ)请画出右上表数据的散点图;
(ⅱ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
 |
| y |
| 129 |
分析:(Ⅰ)样本中,学生为良好的人数为20人,本题即为从100人中抽2人,恰有一人成绩良好的概率,属古典概型,事件空间共有C1002个基本事件,研究事件在其中占了C201•C201个
故概率为
(Ⅱ)(i) 即估计这100个数据的平均数和标准差,先计算等级得分的概率分布列,即加一行频率,再利用期望公式和标准差公式计算即可
(ii)由(i)可知,学生学习能力得分x~N(3,(1.1)2),能力等级在(1.9,4.1)范围内,即X∈(3-1.1,3+1.1),由正态分布的性质,P(μ-σ<x<μ+σ)=0.6826,所以数理学习能力等级在(1.9,4.1)范围内的人数为10000×0.6826=6826
(Ⅲ)(i)先建立平面直角坐标系,再将表中数据作为点的坐标描出即可
(ii)求回归直线方程的方法有两种,一种是使用公式,先设出直线方程,再利用公式求出系数a,b,即可,另一种方法就是最小二乘法,通过求函数的最小值得回归直线的系数a,b,一般情况下我们常使用第一种方法,但要知道公式才行
故概率为
| ||||
|
(Ⅱ)(i) 即估计这100个数据的平均数和标准差,先计算等级得分的概率分布列,即加一行频率,再利用期望公式和标准差公式计算即可
(ii)由(i)可知,学生学习能力得分x~N(3,(1.1)2),能力等级在(1.9,4.1)范围内,即X∈(3-1.1,3+1.1),由正态分布的性质,P(μ-σ<x<μ+σ)=0.6826,所以数理学习能力等级在(1.9,4.1)范围内的人数为10000×0.6826=6826
(Ⅲ)(i)先建立平面直角坐标系,再将表中数据作为点的坐标描出即可
(ii)求回归直线方程的方法有两种,一种是使用公式,先设出直线方程,再利用公式求出系数a,b,即可,另一种方法就是最小二乘法,通过求函数的最小值得回归直线的系数a,b,一般情况下我们常使用第一种方法,但要知道公式才行
解答:解:(Ⅰ)样本中,学生为良好的人数为20人.故从样本中任意抽取 2名学生,则仅有1名学生为良好的概率为
=
(Ⅱ)学生的数理综合学习能力等级分数频率分布如下表:
(ⅰ)总体数据的期望约为:μ=0.5×0.03+1.5×0.17+2.5×0.30+3.5×0.30+4.5×0.17+5.5×0.03=3.0
标准差σ=
=
≈1.1
(ⅱ)由于μ=3,σ≈1.1∴x~N(3,(1.1)2),
∴当x∈(1.9,4.1)时,即x∈(μ-σ,μ+σ )
故数学学习能力等级分数在(1.9,4.1)范围中的概率0.6826.
∴数学学习能力等级在(1.9,4.1)范围中的学生的人数约为10000×0.6826=6826人.
(Ⅲ)
(ⅰ)数据的散点图如下图:

(ⅱ)设线性回归方程为
=bx+a,则
方法一:b=
=
=1.1 a=
-b
=4-1.1×4=-0.4
故回归直线方程为y=1.1x-0.4
方法二:f(a,b)=(2b+a-1.5)2+(3b+a-3)2+(4b+a-3.5)2+(5b+a-5)2+(6b+a-6)2=5a2+40a(b-1)+(2b-1.5)2+(3b-3)2+(4a-3.5)2+(5b-5)2+(6b-6)2
∴a=-
=4(1-b)时,
f(a,b)取得最小值10b2-22b+12.5 即,∴b=1.1,a=-0.4 时f(a,b)取得最小值;
所以线性回归方程为y=1.1x-0.4.
| ||||
|
| 32 |
| 99 |
(Ⅱ)学生的数理综合学习能力等级分数频率分布如下表:
| 等级得分 | (0,1] | (1,2] | (2,3] | (3,4] | (4,5] | (5,6] |
| 人数 | 3 | 17 | 30 | 30 | 17 | 3 |
| 频率 | 0.03 | 0.17 | 0.30 | 0.3 | 0.17 | 0.3 |
标准差σ=
| (0.5-3)2×0.03+(1.5-3)2×0.17+(2.5-3)2×0.3+(3.5-3)2×0.3+ |
. |
| (4.5-3)2×0.17+(5.5-3)2×0.03 |
| 1.29 |
(ⅱ)由于μ=3,σ≈1.1∴x~N(3,(1.1)2),
∴当x∈(1.9,4.1)时,即x∈(μ-σ,μ+σ )
故数学学习能力等级分数在(1.9,4.1)范围中的概率0.6826.
∴数学学习能力等级在(1.9,4.1)范围中的学生的人数约为10000×0.6826=6826人.
(Ⅲ)
(ⅰ)数据的散点图如下图:

(ⅱ)设线性回归方程为
 |
| y |
方法一:b=
| |||||||
|
| 91-80 |
| 90-80 |
. |
| y |
. |
| x |
故回归直线方程为y=1.1x-0.4
方法二:f(a,b)=(2b+a-1.5)2+(3b+a-3)2+(4b+a-3.5)2+(5b+a-5)2+(6b+a-6)2=5a2+40a(b-1)+(2b-1.5)2+(3b-3)2+(4a-3.5)2+(5b-5)2+(6b-6)2
∴a=-
| 40(b-1) |
| 10 |
f(a,b)取得最小值10b2-22b+12.5 即,∴b=1.1,a=-0.4 时f(a,b)取得最小值;
所以线性回归方程为y=1.1x-0.4.
点评:本题考察了概率与统计的知识,综合考察了识图能力,用样本估计总体的数字特征,用样本估计总体的分布,用样本研究变量间的不确定关系的方法运用

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(本小题满分12分)
某市为了对学生的数理(数学与物理)学习能力进行分析,从10000名学生中随机抽出100位学生的数理综合学习能力等级分数(6分制)作为样本,分数频数分布如下表:
|
等级得分 |
|
|
|
|
|
|
|
人数 |
3 |
17 |
30 |
30 |
17 |
3 |
(Ⅰ)如果以能力等级分数大于4分作为良好的标准,从样本中任意抽取2名学生,求恰有1名学生为良好的概率;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值(例如区间 的中点值为1.5)作为代表:
的中点值为1.5)作为代表:
(ⅰ)据此,计算这100名学生数理学习能力等级分数的期望 及标准差
及标准差 (精确到0.1);
(精确到0.1);
(ⅱ) 若总体服从正态分布,以样本估计总体,估计该市这10000名学生中数理学习能力等级在 范围内的人数 .
范围内的人数 .
(Ⅲ)从这10000名学生中任意抽取5名同学,
他们数学与物理单科学习能力等级分
数如下表:


(ⅰ)请画出上表数据的散点图;
(ⅱ)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程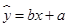 (附参考数据:
(附参考数据: )
)
某市为了对学生的数理(数学与物理)学习能力进行分析,从10000名学生中随机抽出100位学生的数理综合学习能力等级分数(6分制)作为样本,分数频数分布如下表:
(Ⅰ)如果以能力等级分数大于4分作为良好的标准,从样本中任意抽取2名学生,求恰有1名学生为良好的概率;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值(例如区间(1,2]的中点值为1.5)作为代表:
(ⅰ)据此,计算这100名学生数理学习能力等级分数的期望μ及标准差σ(精确到0.1);
(ⅱ) 若总体服从正态分布,以样本估计总体,估计该市这10000名学生中数理学习能力等级在(1.9,4.1)范围内的人数.
(Ⅲ)从这10000名学生中任意抽取5名同学,他们数学与物理单科学习能力等级分数如下表:

(ⅰ)请画出右上表数据的散点图;
(ⅱ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 (附参考数据:
(附参考数据: )
)

| 等级得分 | (0,1] | (1,2] | (2,3] | (3,4] | (4,5] | (5,6] |
| 人数 | 3 | 17 | 30 | 30 | 17 | 3 |
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值(例如区间(1,2]的中点值为1.5)作为代表:
(ⅰ)据此,计算这100名学生数理学习能力等级分数的期望μ及标准差σ(精确到0.1);
(ⅱ) 若总体服从正态分布,以样本估计总体,估计该市这10000名学生中数理学习能力等级在(1.9,4.1)范围内的人数.
(Ⅲ)从这10000名学生中任意抽取5名同学,他们数学与物理单科学习能力等级分数如下表:

(ⅰ)请画出右上表数据的散点图;
(ⅱ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
 (附参考数据:
(附参考数据: )
)





 的中点值为1.5)作为代表:
的中点值为1.5)作为代表: 级分数的期望
级分数的期望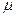 及标准差
及标准差 (精确到0.1);
(精确到0.1);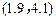 范围内的人数 .
范围内的人数 .

 关于
关于 的线性回归方程
的线性回归方程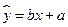 (附参考数据:
(附参考数据: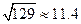 )
)