摘要:由题意知.且.
网址:http://m.1010jiajiao.com/timu_id_281450[举报]
已知无穷数列{an}满足a1=2,数列{(
)an}是各项和等于
的无穷等比数列,其中常数b是正整数.
(1)求无穷等比数列{(
)an}的公比和数列{an}的通项公式;
(2)在无穷等比数列{bn}中,b1=a1,b2=a2,试找出一个b的具体值,使得数列{bn}的任意项都在数列{an}中;试找出一个b的具体值,使得数列{bn}的项不都在数列{an}中,简要说明理由;
(3)对于问题(2)继续进行研究,探究当且仅当b取怎样的值时,数列{bn}的任意项都在数列{an}中,说明理由. 查看习题详情和答案>>
| 1 |
| 2 |
| 2b |
| 2b+2-4 |
(1)求无穷等比数列{(
| 1 |
| 2 |
(2)在无穷等比数列{bn}中,b1=a1,b2=a2,试找出一个b的具体值,使得数列{bn}的任意项都在数列{an}中;试找出一个b的具体值,使得数列{bn}的项不都在数列{an}中,简要说明理由;
(3)对于问题(2)继续进行研究,探究当且仅当b取怎样的值时,数列{bn}的任意项都在数列{an}中,说明理由. 查看习题详情和答案>>
(本题满分12分)已知过点![]() 且斜率为1的直线
且斜率为1的直线![]() 与直线
与直线![]()
交于点![]() .
.
(1)求以![]() 、
、![]() 为焦点且过点
为焦点且过点![]() 的椭圆
的椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上除长轴两端点外的任意一点,试问在
上除长轴两端点外的任意一点,试问在![]() 轴上是否存在两定点
轴上是否存在两定点![]() 、
、![]() 使
使
得直线![]() 、
、![]() 的斜率之积为定值?若存在,请求出定值,并求出所有满足条件的定点
的斜率之积为定值?若存在,请求出定值,并求出所有满足条件的定点![]() 、
、
![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本题满分12分)已知过点![]() 且斜率为1的直线
且斜率为1的直线![]() 与直线
与直线![]()
交于点![]() .
.
(1)求以![]() 、
、![]() 为焦点且过点
为焦点且过点![]() 的椭圆
的椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上除长轴两端点外的任意一点,试问在
上除长轴两端点外的任意一点,试问在![]() 轴上是否存在两定点
轴上是否存在两定点![]() 、
、![]() 使
使
得直线![]() 、
、![]() 的斜率之积为定值?若存在,请求出定值,并求出所有满足条件的定点
的斜率之积为定值?若存在,请求出定值,并求出所有满足条件的定点![]() 、
、
![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
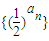 是各项和等于
是各项和等于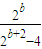 的无穷等比数列,其中常数b是正整数.
的无穷等比数列,其中常数b是正整数.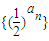 的公比和数列{an}的通项公式;
的公比和数列{an}的通项公式;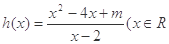 ,且
,且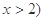 ,函数
,函数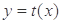 的图象经过点
的图象经过点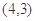 ,且
,且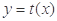 与
与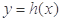 的图象关于直线
的图象关于直线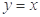 对称,将函数
对称,将函数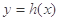 的图象向左平移2个单位后得到函数
的图象向左平移2个单位后得到函数 的图象.
的图象.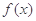 的解析式;
的解析式;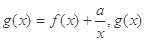 在区间
在区间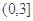 上的值不小于8,求实数
上的值不小于8,求实数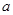 的取值范围.
的取值范围.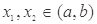 (其中
(其中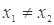 ),有
),有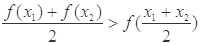 ,称函数
,称函数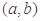 的图象是“下凸的”.判断此题中的函数
的图象是“下凸的”.判断此题中的函数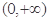 是否是“下凸的”?如果是,给出证明;如果不是,说明理由.
是否是“下凸的”?如果是,给出证明;如果不是,说明理由.