题目内容
已知无穷数列{an}满足a1=2,数列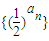 是各项和等于
是各项和等于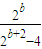 的无穷等比数列,其中常数b是正整数.
的无穷等比数列,其中常数b是正整数.(1)求无穷等比数列
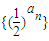 的公比和数列{an}的通项公式;
的公比和数列{an}的通项公式;(2)在无穷等比数列{bn}中,b1=a1,b2=a2,试找出一个b的具体值,使得数列{bn}的任意项都在数列{an}中;试找出一个b的具体值,使得数列{bn}的项不都在数列{an}中,简要说明理由;
(3)对于问题(2)继续进行研究,探究当且仅当b取怎样的值时,数列{bn}的任意项都在数列{an}中,说明理由.
【答案】分析:(1)利用无穷等比数列的求和公式,可得方程,从而求出公比,进而可求数列的通项;
(2)先求出数列{bn}的通项公式,再赋值验证;
(3)当b取奇数时,b3∉{an};当b取偶数时,数列{bn}的任意项都在数列{an}中,再作证明.
解答:解:(1)由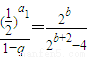 即
即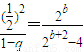 得,
得,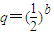 --------------(2分)∴
--------------(2分)∴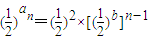 ∴an=2+(n-1)b,n∈N*-----------------------------------------------(5分)
∴an=2+(n-1)b,n∈N*-----------------------------------------------(5分)
(2)∵a1=2,∴a2=2+b,又b1=a1,b2=a2∴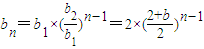 ,n∈N*-------------------(6分)
,n∈N*-------------------(6分)
取b=2,则an=2n,n∈N*,bn=2n,n∈N*∴数列{bn}的任意项都在数列{an}中.------------------------(8分)
取b=1,则an=n+1,n∈N*,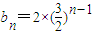 ,n∈N*∴
,n∈N*∴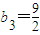 ,∴数列{bn}的项不都在数列{an}中.---------(10分)
,∴数列{bn}的项不都在数列{an}中.---------(10分)
(3)当b取奇数时,b3∉{an};当b取偶数时,数列{bn}的任意项都在数列{an}中.
证明:bn=2×(k+1)n-1=2(Cn-1kn-1+Cn-11kn-2+…+Cn-1n-2k+Cn-1n-1)=2+2k[(Cn-1kn-2+Cn-11kn-3+…+Cn-1n-2+1)-1]
是数列{an}中的第Cn-1kn-2+Cn-11kn-3+…+Cn-1n-2+1项----------------(18分)
点评:本题主要考查无穷等比数列的求和公式,考查数列的通项公式,考查学生分析转化问题的能力,有一定的技巧性.
(2)先求出数列{bn}的通项公式,再赋值验证;
(3)当b取奇数时,b3∉{an};当b取偶数时,数列{bn}的任意项都在数列{an}中,再作证明.
解答:解:(1)由
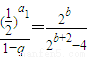 即
即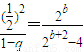 得,
得,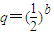 --------------(2分)∴
--------------(2分)∴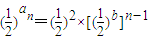 ∴an=2+(n-1)b,n∈N*-----------------------------------------------(5分)
∴an=2+(n-1)b,n∈N*-----------------------------------------------(5分)(2)∵a1=2,∴a2=2+b,又b1=a1,b2=a2∴
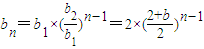 ,n∈N*-------------------(6分)
,n∈N*-------------------(6分)取b=2,则an=2n,n∈N*,bn=2n,n∈N*∴数列{bn}的任意项都在数列{an}中.------------------------(8分)
取b=1,则an=n+1,n∈N*,
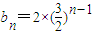 ,n∈N*∴
,n∈N*∴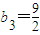 ,∴数列{bn}的项不都在数列{an}中.---------(10分)
,∴数列{bn}的项不都在数列{an}中.---------(10分)(3)当b取奇数时,b3∉{an};当b取偶数时,数列{bn}的任意项都在数列{an}中.
证明:bn=2×(k+1)n-1=2(Cn-1kn-1+Cn-11kn-2+…+Cn-1n-2k+Cn-1n-1)=2+2k[(Cn-1kn-2+Cn-11kn-3+…+Cn-1n-2+1)-1]
是数列{an}中的第Cn-1kn-2+Cn-11kn-3+…+Cn-1n-2+1项----------------(18分)
点评:本题主要考查无穷等比数列的求和公式,考查数列的通项公式,考查学生分析转化问题的能力,有一定的技巧性.

练习册系列答案
相关题目