摘要：13．质点的运动方程是(其中).则质点在t＝2时刻的速度为 .
网址：http://m.1010jiajiao.com/timu_id_24617[举报]
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
A
C
C
B
D
B
A
D
A
C
D
D
二、填空题
13、45 14、
15、
16、0.94 17、
18、
三、解答题
19、解：
f(x)=
?(
－1) 
f(x)=(2x+1)=2?0+1=1
∴
20、解：（1）当a＝2时，A＝（2，7），B＝（4，5）∴ A
B＝（4，5）
（2）∵ B＝（
当a＜
时，A＝（
A，必须
，此时a＝－1；
当a＝时，A＝
，使BA的a不存在；
当a＞时，A＝（2，A，必须
，此时1≤a≤3.
综上可知，使BA的实数a的取值范围为[1，3]∪{－1}
21、解：（1）ξ可能的取值为0，1，2，3．
P(ξ＝0)＝?＝＝ P(ξ＝1)＝?＋?＝
P(ξ＝2)＝?＋?＝ P(ξ＝3)＝?＝．
ξ的分布列为
ξ
0
1
2
3
P
数学期望为Eξ＝1.2．
(2)所求的概率为
p＝P(ξ≥2)＝P(ξ＝2)＋P(ξ＝3)＝＋＝
22、解：
，（2分）
因为函数
在
处的切线斜率为-3，
所以
，即
，
1
又
得
。
2
（1）函数在
时有极值，所以
， 3
解123得
，
所以
.
（2）因为函数在区间
上单调递增，所以导函数
在区间上的值恒大于或等于零，
则
得
，所以实数
的取值范围为
.
如右图所示，定义在D上的函数f（x），如果满足：对?x∈D，常数A，都有f（x）≥A成立，则称函数f（x）在D上有下界，其中A称为函数的下界．（提示：图中的常数A可以是正数，也可以是负数或零）（1）试判断函数f(x)=x3+
| 48 |
| x |
（2）已知某质点的运动方程为S(t)=at-2
| t+1 |
| 1 |
| 2 |
如图（1）示，定义在D上的函数f（x），如果满足：对?x∈D，?常数A，都有f（x）≥A成立，则称函数f（x）在D上有下界，其中A称为函数的下界．（提示：图（1）、（2）中的常数A、B可以是正数，也可以是负数或零）
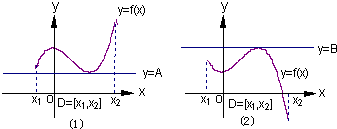
（Ⅰ）试判断函数f（x）=x3+
在（0，+∞）上是否有下界？并说明理由；
（Ⅱ）又如具有如图（2）特征的函数称为在D上有上界．请你类比函数有下界的定义，给出函数f（x）在D上有上界的定义，并判断（Ⅰ）中的函数在（-∞，0）上是否有上界？并说明理由；
（Ⅲ）已知某质点的运动方程为S（t）=at-2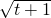
，要使在t∈[0，+∞）上的每一时刻该质点的瞬时速度是以A=
为下界的函数，求实数a的取值范围．
查看习题详情和答案>>
如图（1）示，定义在D上的函数f（x），如果满足：对?x∈D，?常数A，都有f（x）≥A成立，则称函数f（x）在D上有下界，其中A称为函数的下界．（提示：图（1）、（2）中的常数A、B可以是正数，也可以是负数或零）
（Ⅰ）试判断函数f（x）=x3+
在（0，+∞）上是否有下界？并说明理由；
（Ⅱ）又如具有如图（2）特征的函数称为在D上有上界．请你类比函数有下界的定义，给出函数f（x）在D上有上界的定义，并判断（Ⅰ）中的函数在（-∞，0）上是否有上界？并说明理由；
（Ⅲ）已知某质点的运动方程为S（t）=at-2
，要使在t∈[0，+∞）上的每一时刻该质点的瞬时速度是以A=
为下界的函数，求实数a的取值范围．
查看习题详情和答案>>
（Ⅰ）试判断函数f（x）=x3+
在（0，+∞）上是否有下界？并说明理由；（Ⅱ）又如具有如图（2）特征的函数称为在D上有上界．请你类比函数有下界的定义，给出函数f（x）在D上有上界的定义，并判断（Ⅰ）中的函数在（-∞，0）上是否有上界？并说明理由；
（Ⅲ）已知某质点的运动方程为S（t）=at-2
，要使在t∈[0，+∞）上的每一时刻该质点的瞬时速度是以A=为下界的函数，求实数a的取值范围．查看习题详情和答案>>
，如果满足：
，
常数
，都有
≤M成立，则称
在[1，3]上是不是有界函数？请给出证明；
，要使在
上的每一时刻的瞬时速度是以M=1为上界的有界函数，求实数a的取值范围.
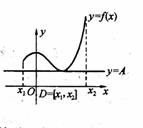（本题满分12）如右图所示，定义在D上的函数
，如果满足：对
，
常数A，都有
成立，则称函数
在
上是否有下界？并说明理由；
，要使在
上的每一时刻该质点的瞬时速度是以
为下界的函数，求实数a的取值范围．