题目内容
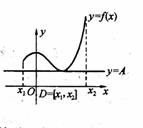（本题满分12）如右图所示，定义在D上的函数
，如果满足：对
，
常数A，都有
成立，则称函数在D上有下界，其中A称为函数的下界．（提示：图中的常数A可以是正数，也可以是负数或零）
（1）试判断函数
在
上是否有下界？并说明理由；
（2）已知某质点的运动方程为
，要使在
上的每一时刻该质点的瞬时速度是以
为下界的函数，求实数a的取值范围．
解析：（1）求导或基本不等式的推广都可以证明有下界（A=32）存在．………………6分
（2）质点在
上的每一时刻该质点的瞬时速度
。
依题意得对
有
即：
对恒成立 ．所以 
． ………………12分
练习册系列答案
相关题目
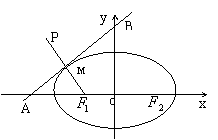
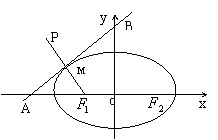
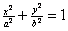（a>b>0）的左、右焦点分别是
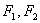，离心率为e.直线L：y=ex+a与x轴、y轴分别交于A、B点，M是直线L与椭圆C的一个公共点，P是点
关于直线L的对称点。设
。
=1-
； （Ⅱ）确定
是等腰三角形。
（a>b>0）的左、右焦点分别是
，离心率为e.直线L：y=ex+a与x轴、y轴分别交于A、B点，M是直线L与椭圆C的一个公共点，P是点
关于直线L的对称点。设
。
=1-
； （Ⅱ）确定
是等腰三角形。
（a>b>0）的左、右焦点分别是
，离心率为e.直线L：y=ex+a与x轴、y轴分别交于A、B点，M是直线L与椭圆C的一个公共点，P是点
关于直线L的对称点。设
。
=1-
；
（Ⅱ）确定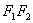
是等腰三角形。