题目内容
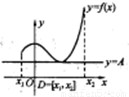
定义在D上的函数![]() ,如果满足:
,如果满足:![]() ,
,![]() 常数
常数![]() ,都有
,都有![]() ≤M成立,则称
≤M成立,则称![]() 是D上的有界函数,其中M称为函数的上界.
是D上的有界函数,其中M称为函数的上界.
(Ⅰ)试判断函数![]() 在[1,3]上是不是有界函数?请给出证明;
在[1,3]上是不是有界函数?请给出证明;
(Ⅱ)若已知质点的运动方程为![]() ,要使在
,要使在![]() 上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
解:(Ⅰ)∵![]() ,当
,当![]() 时,
时,![]() .
.
∴![]() 在[1,3]上是增函数.
在[1,3]上是增函数.
∴当![]() 时,
时,![]() ≤
≤![]() ≤
≤![]() ,即 -2≤
,即 -2≤![]() ≤26.
≤26.
∴存在常数M=26,使得![]() ,都有
,都有![]() ≤M成立.
≤M成立.
故函数![]() 是[1,3]上的有界函数.
是[1,3]上的有界函数.
(Ⅱ)∵![]() . 由
. 由![]() ≤1,得
≤1,得![]() ≤1
≤1
∴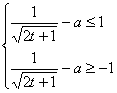
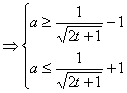
令![]() ,则
,则![]() .
.
当![]() 时,有
时,有![]() ,
,
∴![]() 在[0,+∞
在[0,+∞![]() 上单调递减.
上单调递减.
故当t=0 时,有![]() ;
;
又![]() ,当t→+∞时,
,当t→+∞时,![]() →0,
→0,
∴ ![]() ,从而有
,从而有![]() ≤0,且
≤0,且![]() . ∴0≤a≤1;
. ∴0≤a≤1;
故所求a的取值范围为0≤a≤1.

练习册系列答案
相关题目

 如右图所示,定义在D上的函数f(x),如果满足:对?x∈D,常数A,都有f(x)≥A成立,则称函数f(x)在D上有下界,其中A称为函数的下界.(提示:图中的常数A可以是正数,也可以是负数或零)
如右图所示,定义在D上的函数f(x),如果满足:对?x∈D,常数A,都有f(x)≥A成立,则称函数f(x)在D上有下界,其中A称为函数的下界.(提示:图中的常数A可以是正数,也可以是负数或零)
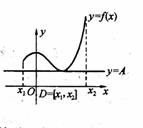 (本题满分12)如右图所示,定义在D上的函数
(本题满分12)如右图所示,定义在D上的函数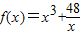 在(0,+∞)上是否有下界?并说明理由;
在(0,+∞)上是否有下界?并说明理由;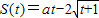 ,要使在t∈[0,+∞)上的每一时刻该质点的瞬时速度是以
,要使在t∈[0,+∞)上的每一时刻该质点的瞬时速度是以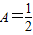 为下界的函数,求实数a的取值范围.
为下界的函数,求实数a的取值范围.