摘要:(Ⅱ)解 作交于.
网址:http://m.1010jiajiao.com/timu_id_24123[举报]
 (选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
(选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.A.选修4-1:几何证明选讲
如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于N,过
N点的切线交CA的延长线于P.
(1)求证:PM2=PA•PC;
(2)若⊙O的半径为2
| 3 |
| 3 |
B.选修4-2:矩阵与变换
曲线x2+4xy+2y2=1在二阶矩阵M=
|
C.选修4-4:坐标系与参数方程
在极坐标系中,圆C的极坐标方程为ρ=
| 2 |
| π |
| 4 |
|
D.选修4-5:不等式选讲
设a,b,c均为正实数.
(1)若a+b+c=1,求a2+b2+c2的最小值;
(2)求证:
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
(考生注意:请在下列两题中任选一题作答,如果多做则按所做的第一题评分)
(1)在极坐标系中,若过点(1,0)且与极轴垂直的直线交曲线ρ=4cosθ于A、B两点,则|AB|=
(2)已知方程|2x-1|-|2x+1|=a+1有实数解,则a的取值范围为
查看习题详情和答案>>
(1)在极坐标系中,若过点(1,0)且与极轴垂直的直线交曲线ρ=4cosθ于A、B两点,则|AB|=
2
| 3 |
2
| 3 |
(2)已知方程|2x-1|-|2x+1|=a+1有实数解,则a的取值范围为
[-3,-1)
[-3,-1)
.(选修4-4:坐标系与参数方程)
已知椭圆的长轴长为6,焦距F1F2=4
,过椭圆左焦点F1作一直线,交椭圆于两点M、N,设∠F2F1M=α(0≤α<π),当α为何值时,MN与椭圆短轴长相等?(用极坐标或参数方程方程求解)
查看习题详情和答案>>
已知椭圆的长轴长为6,焦距F1F2=4
| 2 |
(1)若椭圆的方程是:
+
=1(a>b>0),它的左、右焦点依次为F1、F2,P是椭圆上异于长轴端点的任意一点.在此条件下我们可以提出这样一个问题:“设△PF1F2的过P角的外角平分线为l,自焦点F2引l的垂线,垂足为Q,试求Q点的轨迹方程?”
对该问题某同学给出了一个正确的求解,但部分解答过程因作业本受潮模糊了,我们在
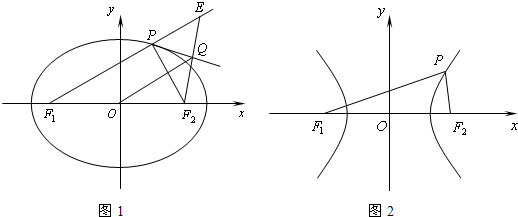
这些模糊地方划了线,请你将它补充完整.
解:延长F2Q 交F1P的延长线于E,据题意,
E与F2关于l对称,所以|PE|=|PF2|.
所以|EF1|=|PF1|+|PE|=|PF1|+|PF2|= ,
在△EF1F2中,显然OQ是平行于EF1的中位线,
所以|OQ|=
|EF1|= ,
注意到P是椭圆上异于长轴端点的点,所以Q点的轨迹是 ,
其方程是: .
(2)如图2,双曲线的方程是:
-
=1(a,b>0),它的左、右焦点依次为F1、F2,P是双曲线上异于实轴端点的任意一点.请你试着提出与(1)类似的问题,并加以证明.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
对该问题某同学给出了一个正确的求解,但部分解答过程因作业本受潮模糊了,我们在
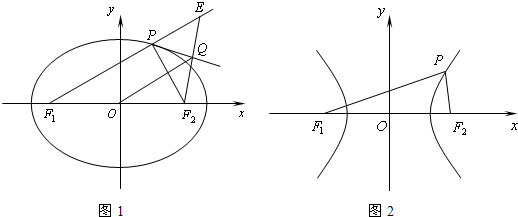
这些模糊地方划了线,请你将它补充完整.
解:延长F2Q 交F1P的延长线于E,据题意,
E与F2关于l对称,所以|PE|=|PF2|.
所以|EF1|=|PF1|+|PE|=|PF1|+|PF2|=
在△EF1F2中,显然OQ是平行于EF1的中位线,
所以|OQ|=
| 1 |
| 2 |
注意到P是椭圆上异于长轴端点的点,所以Q点的轨迹是
其方程是:
(2)如图2,双曲线的方程是:
| x2 |
| a2 |
| y2 |
| b2 |
 (本题为选做题,请在下列三题中任选一题作答)
(本题为选做题,请在下列三题中任选一题作答)