题目内容
 (本题为选做题,请在下列三题中任选一题作答)
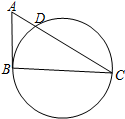
(本题为选做题,请在下列三题中任选一题作答)A(《几何证明选讲》选做题).如图:直角三角形ABC中,∠B=90°,AB=4,以BC为直径的圆交边AC于点D,AD=2,则∠C的大小为
30°
30°
.B(《坐标系与参数方程选讲》选做题).已知直线的极坐标方程为ρsin(θ+
| π |
| 4 |
| ||
| 2 |
| 7π |
| 4 |
| ||
| 2 |
| ||
| 2 |
C(不等式选讲)不等式|x-1|+|x|<3的解集是
(-1,2)
(-1,2)
.分析:A、利用切割线定理,求AC长,进而可求∠C的值;
B、将极坐标化为直角坐标,再利用点到直线的距离公式,即可求解;
C、利用绝对值的几何意义,分类讨论,即可得到结论.
B、将极坐标化为直角坐标,再利用点到直线的距离公式,即可求解;
C、利用绝对值的几何意义,分类讨论,即可得到结论.
解答:解:A、由题意,42=2×AC,∴AC=8,∴sin∠C=
=
,∴∠C=30°;
B、直线的极坐标方程为ρsin(θ+
)=
,可化为x+y-1=0,点A(2,
)可化为(
,-
),由点到直线的距离公式可得d=
=
;
C、由题意可得
或
或
∴-1<x<0或0≤x≤1或1<x<2
∴-1<x<2
故答案为:30°;
;(-1,2)
| AB |
| AC |
| 1 |
| 2 |
B、直线的极坐标方程为ρsin(θ+
| π |
| 4 |
| ||
| 2 |
| 7π |
| 4 |
| 2 |
| 2 |
| 1 | ||
|
| ||
| 2 |
C、由题意可得
|
|
|
∴-1<x<0或0≤x≤1或1<x<2
∴-1<x<2
故答案为:30°;
| ||
| 2 |
点评:本题是选做题,考查圆的切线,考查极坐标知识,考查绝对值不等式,综合性强.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目

 (本题为选做题,请在下列三题中任选一题作答)
(本题为选做题,请在下列三题中任选一题作答)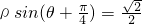 ,则点A(2,
,则点A(2, )到这条直线的距离为________.
)到这条直线的距离为________. (t为参数)距离的最大值为 .
(t为参数)距离的最大值为 .

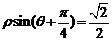 ,则点
,则点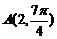 到这条直线的距离
到这条直线的距离