题目内容
(1)若椭圆的方程是:| x2 |
| a2 |
| y2 |
| b2 |
对该问题某同学给出了一个正确的求解,但部分解答过程因作业本受潮模糊了,我们在
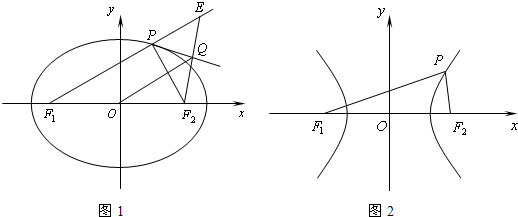
这些模糊地方划了线,请你将它补充完整.
解:延长F2Q 交F1P的延长线于E,据题意,
E与F2关于l对称,所以|PE|=|PF2|.
所以|EF1|=|PF1|+|PE|=|PF1|+|PF2|=
在△EF1F2中,显然OQ是平行于EF1的中位线,
所以|OQ|=
| 1 |
| 2 |
注意到P是椭圆上异于长轴端点的点,所以Q点的轨迹是
其方程是:
(2)如图2,双曲线的方程是:
| x2 |
| a2 |
| y2 |
| b2 |
分析:(1)根据题意:延长F2Q 交F1P的延长线于E,E与F2关于l对称,所以|PE|=|PF2|.所以|EF1|=|PF1|+|PE|=|PF1|+|PF2|=2a,在△EF1F2中,显然OQ是平行于EF1的中位线,所以|OQ|=
|EF1|=a,注意到P是椭圆上异于长轴端点的点,易得答案.
(2)问题:如图,双曲线的方程是:
-
=1(a,b>0),它的左、右焦点依次为F1、F2,P是双曲线上异于实轴端点的任意一点.设△PF1F2的过P角的内角平分线为l,自焦点F1引l的垂线,垂足为Q,试求Q点的轨迹方程?并加以证明.利用与(1)类似的方法进行证明即可.
| 1 |
| 2 |
(2)问题:如图,双曲线的方程是:
| x2 |
| a2 |
| y2 |
| b2 |
解答: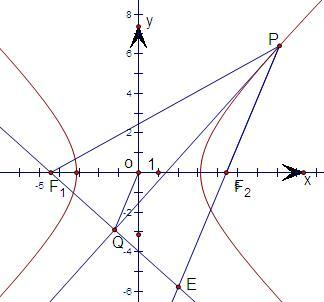 解:(1)根据题意:延长F2Q 交F1P的延长线于E,
解:(1)根据题意:延长F2Q 交F1P的延长线于E,
E与F2关于l对称,所以|PE|=|PF2|.
所以|EF1|=|PF1|+|PE|=|PF1|+|PF2|=2a,
在△EF1F2中,显然OQ是平行于EF1的中位线,
所以|OQ|=
|EF1|=a,
注意到P是椭圆上异于长轴端点的点,所以Q点的轨迹是 圆(不含椭圆长轴端点),
其方程是:x2+y2=a2(x≠±a)
故答案为:2a,a,圆,x2+y2=a2(x≠±a).
(2)问题:如图,双曲线的方程是:
-
=1(a,b>0),它的左、右焦点依次为F1、F2,P是双曲线上异于实轴端点的任意一点.设△PF1F2的过P角的内角平分线为l,自焦点F1引l的垂线,垂足为Q,试求Q点的轨迹方程?并加以证明.
证明:延长F1Q 交F2P的延长线于E,根据题意,
E与F1关于l对称,所以|PE|=|PF1|.
所以|EF1|=|PF1|-|PE|=|PF1|-|PF2|=2a,
在△EF1F2中,显然OQ是平行于EF2的中位线,
所以|OQ|=
|EF2|=a,
注意到P是椭圆上异于实轴端点的点,所以Q点的轨迹是 圆(不含双曲线实轴端点),
其方程是:x2+y2=a2(x≠±a)
 解:(1)根据题意:延长F2Q 交F1P的延长线于E,
解:(1)根据题意:延长F2Q 交F1P的延长线于E,E与F2关于l对称,所以|PE|=|PF2|.
所以|EF1|=|PF1|+|PE|=|PF1|+|PF2|=2a,
在△EF1F2中,显然OQ是平行于EF1的中位线,
所以|OQ|=
| 1 |
| 2 |
注意到P是椭圆上异于长轴端点的点,所以Q点的轨迹是 圆(不含椭圆长轴端点),
其方程是:x2+y2=a2(x≠±a)
故答案为:2a,a,圆,x2+y2=a2(x≠±a).
(2)问题:如图,双曲线的方程是:
| x2 |
| a2 |
| y2 |
| b2 |
证明:延长F1Q 交F2P的延长线于E,根据题意,
E与F1关于l对称,所以|PE|=|PF1|.
所以|EF1|=|PF1|-|PE|=|PF1|-|PF2|=2a,
在△EF1F2中,显然OQ是平行于EF2的中位线,
所以|OQ|=
| 1 |
| 2 |
注意到P是椭圆上异于实轴端点的点,所以Q点的轨迹是 圆(不含双曲线实轴端点),
其方程是:x2+y2=a2(x≠±a)
点评:本题考查双曲线和椭圆的标准方程和简单性质,定义的应用,得出OQ是平行于EF2的中位线是解题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知椭圆
已知椭圆