题目内容
 (选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
(选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.A.选修4-1:几何证明选讲
如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于N,过
N点的切线交CA的延长线于P.
(1)求证:PM2=PA•PC;
(2)若⊙O的半径为2
| 3 |
| 3 |
B.选修4-2:矩阵与变换
曲线x2+4xy+2y2=1在二阶矩阵M=
|
C.选修4-4:坐标系与参数方程
在极坐标系中,圆C的极坐标方程为ρ=
| 2 |
| π |
| 4 |
|
D.选修4-5:不等式选讲
设a,b,c均为正实数.
(1)若a+b+c=1,求a2+b2+c2的最小值;
(2)求证:
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
分析:A:(1)做出辅助线连接ON,根据切线得到直角,根据垂直得到直角,即∠ONB+∠BNP=90°且∠OBN+∠BMO=90°,根据同角的余角相等,得到角的相等关系,得到结论.
(2)本题是一个求线段长度的问题,在解题时,应用相交弦定理,即BM•MN=CM•MA,代入所给的条件,得到要求线段的长.
B:设P(x,y)为曲线x2-2y2=1上任意一点,P′(x′,y′)为曲线x2+4xy+2y2=1上与P对应的点,所以
,由此能够求出a和b的值.
C:先两边同乘以ρ,利用公式即可得到圆的圆心和半径,再将参数方程化为普通方程,结合直角坐标系下的点到直线的距离公式求解即得.
D:(1)根据(a2+b2+c2)(12+12+12)≥(a+b+c)2=1,可得 a2+b2+c2 的最小值为
.
(2)由a,b,c均为正实数,可得
(
+
)≥
≥
,同理
(
+
)≥
,
(
+
)≥
,相加可得不等式成立.
(2)本题是一个求线段长度的问题,在解题时,应用相交弦定理,即BM•MN=CM•MA,代入所给的条件,得到要求线段的长.
B:设P(x,y)为曲线x2-2y2=1上任意一点,P′(x′,y′)为曲线x2+4xy+2y2=1上与P对应的点,所以
|
C:先两边同乘以ρ,利用公式即可得到圆的圆心和半径,再将参数方程化为普通方程,结合直角坐标系下的点到直线的距离公式求解即得.
D:(1)根据(a2+b2+c2)(12+12+12)≥(a+b+c)2=1,可得 a2+b2+c2 的最小值为
| 1 |
| 3 |
(2)由a,b,c均为正实数,可得
| 1 |
| 2 |
| 1 |
| 2a |
| 1 |
| 2b |
| 1 | ||
2
|
| 1 |
| a+b |
| 1 |
| 2 |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| 2 |
| 1 |
| 2c |
| 1 |
| 2a |
| 1 |
| c+a |
解答: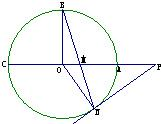 解:A:(1)证明:连接ON,因为PN切⊙O于N,
解:A:(1)证明:连接ON,因为PN切⊙O于N,
∴∠ONP=90°,
∴∠ONB+∠BNP=90°
∵OB=ON,
∴∠OBN=∠ONB
因为OB⊥AC于O,
∴∠OBN+∠BMO=90°,
故∠BNP=∠BMO=∠PMN,PM=PN
∴PM2=PN2=PA•PC
(2)∵OM=2,BO=2
,BM=4
∵BM•MN=CM•MA=(2
+2)(2
-2)(2
-2)=8,
∴MN=2.
B:(1)设P(x,y)为曲线x2-2y2=1上任意一点,
P′(x′,y′)为曲线x2+4xy+2y2=1上与P对应的点,
则
=
,
即
,
代入(x′+ay′)2-2(bx′+y′)2=1,
得(1-2b2)x'2+(2a-4b)x′y′+(a2-2)y'2=1,
∵方程x2+4xy+2y2=1,
∴
,
解得a=2,b=0.
C:⊙C的方程化为ρ=cosθ-sinθ,两边同乘以ρ,得ρ2=ρcosθ-ρsinθ
由ρ2=x2+y2,x=ρcosθ,y=ρsinθ,
得x2+y2-x+y=0…(5分)
其圆心C坐标为(
,-
),半径r=
,
又直线l的普通方程为3x+4y+1=0,
∴圆心C到直线l的距离d=
=
,
∴弦长AB=2
=
…(10分)
D:(1)因为a,b,c 均为正实数,由柯西不等式得,
(a2+b2+c2)(12+12+12)≥(a+b+c)2=1,当且仅当a=b=c=
时等号成立,
∴a2+b2+c2 的最小值为
. …5分
证明:(2)∵a,b,c均为正实数,
∴可得
(
+
)≥
≥
,
同理
(
+
)≥
,
(
+
)≥
,
三个不等式相加得
+
+
≥
+
+
,当且仅当a=b=c时等号成立.…10分
 解:A:(1)证明:连接ON,因为PN切⊙O于N,
解:A:(1)证明:连接ON,因为PN切⊙O于N,∴∠ONP=90°,
∴∠ONB+∠BNP=90°
∵OB=ON,
∴∠OBN=∠ONB
因为OB⊥AC于O,
∴∠OBN+∠BMO=90°,
故∠BNP=∠BMO=∠PMN,PM=PN
∴PM2=PN2=PA•PC
(2)∵OM=2,BO=2
| 3 |
∵BM•MN=CM•MA=(2
| 3 |
| 3 |
| 3 |
∴MN=2.
B:(1)设P(x,y)为曲线x2-2y2=1上任意一点,
P′(x′,y′)为曲线x2+4xy+2y2=1上与P对应的点,
则
|
|
|
即
|
代入(x′+ay′)2-2(bx′+y′)2=1,
得(1-2b2)x'2+(2a-4b)x′y′+(a2-2)y'2=1,
∵方程x2+4xy+2y2=1,
∴
|
解得a=2,b=0.
C:⊙C的方程化为ρ=cosθ-sinθ,两边同乘以ρ,得ρ2=ρcosθ-ρsinθ
由ρ2=x2+y2,x=ρcosθ,y=ρsinθ,
得x2+y2-x+y=0…(5分)
其圆心C坐标为(
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
又直线l的普通方程为3x+4y+1=0,
∴圆心C到直线l的距离d=
|
| ||
|
| 1 |
| 10 |
∴弦长AB=2
|
| 7 |
| 5 |
D:(1)因为a,b,c 均为正实数,由柯西不等式得,
(a2+b2+c2)(12+12+12)≥(a+b+c)2=1,当且仅当a=b=c=
| 1 |
| 3 |
∴a2+b2+c2 的最小值为
| 1 |
| 3 |
证明:(2)∵a,b,c均为正实数,
∴可得
| 1 |
| 2 |
| 1 |
| 2a |
| 1 |
| 2b |
| 1 | ||
2
|
| 1 |
| a+b |
同理
| 1 |
| 2 |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| 2 |
| 1 |
| 2c |
| 1 |
| 2a |
| 1 |
| c+a |
三个不等式相加得
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
点评:考查切割线定理、用综合法证明不等式、圆的极坐标方程、参数方程与普通方程的互化,点到直线的距离公式等.要求学生能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.属于中等题.

练习册系列答案
相关题目
 选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.
选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤. 选做题(在A、B、C、D四小题中只能选做两题,并将选作标记用2B铅笔涂黑,每小题10分,共20分,请在答题指定区域内作答,解答时应写出文字说明、证明过程或演算步骤).
选做题(在A、B、C、D四小题中只能选做两题,并将选作标记用2B铅笔涂黑,每小题10分,共20分,请在答题指定区域内作答,解答时应写出文字说明、证明过程或演算步骤).