摘要:∵VB-CMN=VN-CMB.NE⊥平面CMB.∴S△CMN?h=S△CMB?NE.
网址:http://m.1010jiajiao.com/timu_id_20342[举报]
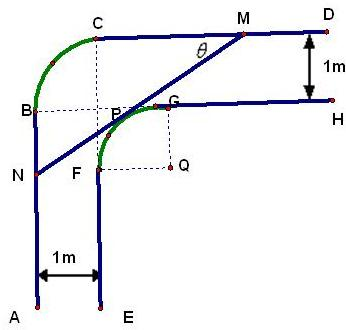 一走廊拐角下的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1m.
一走廊拐角下的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1m.(1)若水平放置的木棒MN的两个端点M、N分别在外壁CD和AB上,且木棒与内壁圆弧相切于点P.设∠CMN=θ(rad),试用θ表示木棒MN和长度f(θ).
(2)若一根水平放置的木棒能通过该走廊拐角处,求木棒长度的最大值. 查看习题详情和答案>>
规定
=
,其中x∈R,m是正整数,且
=1,这是组合数
(n、m是正整数,且m≤n)的一种推广.
(1)求
的值;
(2)设x>0,当x为何值时,
取得最小值?
(3)组合数的两个性质;①
=
;②
+
=
.是否都能推广到
(x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
查看习题详情和答案>>
| C | m x |
| x(x-1)…(x-m+1) |
| m! |
| C | 0 x |
| C | m n |
(1)求
| C | 3 -15 |
(2)设x>0,当x为何值时,
| ||
(
|
(3)组合数的两个性质;①
| C | m n |
| C | n-m n |
| C | m n |
| C | m-1 n |
| C | m n+1 |
| C | m x |
已知M是正四面体ABCD棱AB的中点,N是棱CD的中点,则下列结论中,正确的个数有( )
(1)MN⊥AB;
(2)VA-MCD=VB-MCD;
(3)平面CDM⊥平面ABN;
(4)CM与AN是相交直线.
(1)MN⊥AB;
(2)VA-MCD=VB-MCD;
(3)平面CDM⊥平面ABN;
(4)CM与AN是相交直线.
查看习题详情和答案>>
 在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2
在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2