��Ŀ����
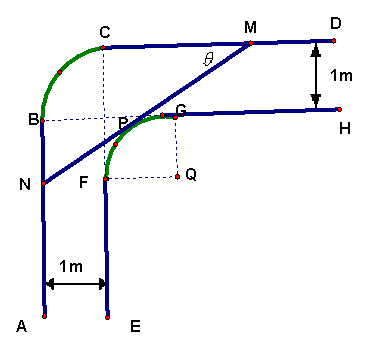
 һ���ȹս��µĺ������ͼ��ʾ����֪�ڱ�FG�����BC���ǰ뾶Ϊ1m���ķ�֮һԲ����AB��DC�ֱ���Բ��BC������B��C���㣬EF��AB��GH��CD��������ƽ��ǽ�ڼ�����ȿ��ȶ���1m��
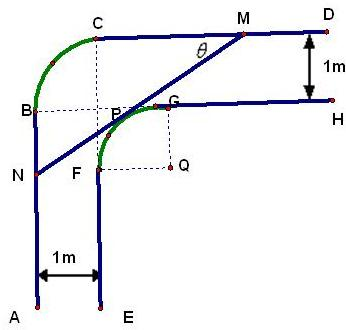
һ���ȹս��µĺ������ͼ��ʾ����֪�ڱ�FG�����BC���ǰ뾶Ϊ1m���ķ�֮һԲ����AB��DC�ֱ���Բ��BC������B��C���㣬EF��AB��GH��CD��������ƽ��ǽ�ڼ�����ȿ��ȶ���1m����1����ˮƽ���õ�ľ��MN�������˵�M��N�ֱ������CD��AB�ϣ���ľ�����ڱ�Բ�������ڵ�P�����CMN=�ȣ�rad�������æȱ�ʾľ��MN�ͳ���f���ȣ���
��2����һ��ˮƽ���õ�ľ����ͨ�������ȹսǴ�����ľ�����ȵ����ֵ��
��������1����ͼ����Բ��FG���ڵ�Բ��Բ��ΪQ����Q����CD���ߣ�����Ϊ��T���ҽ�MN�����ӳ�������S��������PQ���ٹ�N����TQ�Ĵ��ߣ�����ΪW����Rt��NWS����NW�͡�SNW��ʾ��NS����Rt��QPS����PQ�͡�PQS��ʾ��QS��Ȼ��ֱ�S���߶�TG�Ϻ����߶�GT���ӳ����Ϸֱ��ʾ��TS=QT-QS��Ȼ����Rt��STM�б�ʾ��MS������MN=NS+MS���MN�ı���ʽ��f���ȣ��ı���ʽ��
��2�����sin��+cos��=t����sin��cos�ȿ���t��ʾ����Ȼ��ɵ�f���ȣ�����t�ı���ʽ���Ժ�������������t�ķ�Χ�жϳ�������С��0�ƶϳ�����Ϊ����������������t�ķ�Χ��ú�������Сֵ��
��2�����sin��+cos��=t����sin��cos�ȿ���t��ʾ����Ȼ��ɵ�f���ȣ�����t�ı���ʽ���Ժ�������������t�ķ�Χ�жϳ�������С��0�ƶϳ�����Ϊ����������������t�ķ�Χ��ú�������Сֵ��
���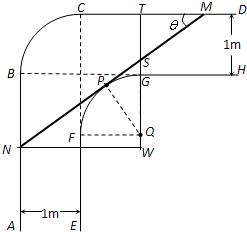 �⣺��1����ͼ����Բ��FG���ڵ�Բ��Բ��ΪQ����Q����CD���ߣ�����Ϊ��T���ҽ�MN�����ӳ�������S��������PQ���ٹ�N����TQ�Ĵ��ߣ�����ΪW��
�⣺��1����ͼ����Բ��FG���ڵ�Բ��Բ��ΪQ����Q����CD���ߣ�����Ϊ��T���ҽ�MN�����ӳ�������S��������PQ���ٹ�N����TQ�Ĵ��ߣ�����ΪW��
��Rt��NWS�У���ΪNW=2����SNW=�ȣ�
����NS=
��
��ΪMN��Բ��FG���ڵ�P������PQ��MN��
��Rt��QPS����ΪPQ=1����PQS=�ȣ�
����QS=
��QT-QS=2-
��
����M���߶�TD�ϣ���S���߶�TG�ϣ���TS=QT-QS��
��Rt��STM��MS=
=
��
���MN=NS+MS=NS+
��
����M���߶�CT�ϣ�����S���߶�GT���ӳ����ϣ���TS=QS-QT��
��Rt��STM��MS=
=
��
���MN=NS-MS=NS-
=NS+
��
f���ȣ�=MN=NS+
=
+(
-
)=
(0���ȣ�
)��
��2����sin��+cos��=t (1��t��
)����sin��cos��=
��
���f(��)=g(t)=
����Ϊg��(t)=-
����1��t��
������g�䣨t����0�������
��˺���g(t)=
��t��(1��
]�Ǽ�����������g(t)min=g(
)=4
-2��
��MNmin=4
-2��
��һ��ˮƽ���õ�ľ������ͨ�������ȹսǴ������䳤�ȵ����ֵΪ4
-2��
 �⣺��1����ͼ����Բ��FG���ڵ�Բ��Բ��ΪQ����Q����CD���ߣ�����Ϊ��T���ҽ�MN�����ӳ�������S��������PQ���ٹ�N����TQ�Ĵ��ߣ�����ΪW��
�⣺��1����ͼ����Բ��FG���ڵ�Բ��Բ��ΪQ����Q����CD���ߣ�����Ϊ��T���ҽ�MN�����ӳ�������S��������PQ���ٹ�N����TQ�Ĵ��ߣ�����ΪW����Rt��NWS�У���ΪNW=2����SNW=�ȣ�
����NS=
| 2 |
| cos�� |
��ΪMN��Բ��FG���ڵ�P������PQ��MN��
��Rt��QPS����ΪPQ=1����PQS=�ȣ�
����QS=
| 1 |
| cos�� |
| 1 |
| cos�� |
����M���߶�TD�ϣ���S���߶�TG�ϣ���TS=QT-QS��
��Rt��STM��MS=
| TS |
| sin�� |
| QT-QS |
| sin�� |
���MN=NS+MS=NS+
| QT-QS |
| sin�� |
����M���߶�CT�ϣ�����S���߶�GT���ӳ����ϣ���TS=QS-QT��
��Rt��STM��MS=
| TS |
| sin�� |
| QS-QT |
| sin�� |
���MN=NS-MS=NS-
| QS-QT |
| sin�� |
| QT-QS |
| sin�� |
f���ȣ�=MN=NS+
| QT-QS |
| sin�� |
| 2 |
| cos�� |
| 2 |
| sin�� |
| 1 |
| sin��cos�� |
| 2(sin��+cos��)-1 |
| sin��cos�� |
| �� |
| 2 |
��2����sin��+cos��=t (1��t��
| 2 |
| t2-1 |
| 2 |
���f(��)=g(t)=
| 4t-2 |
| t2-1 |
| 4(t2-t+1) |
| (t2-1)2 |
| 2 |
��˺���g(t)=
| 4t-2 |
| t2-1 |
| 2 |
| 2 |
| 2 |
��MNmin=4
| 2 |
��һ��ˮƽ���õ�ľ������ͨ�������ȹսǴ������䳤�ȵ����ֵΪ4
| 2 |
������������Ҫ�����˽������ε�ʵ��Ӧ�ã�������ѧ����������ͽ�����������������������������

��ϰ��ϵ�д�
�����Ŀ