网址:http://m.1010jiajiao.com/timu_id_19811[举报]
一、选择题
1.D 2.A 3.A 4.B 5.B 6.C 7.C 8.C 9.C 10.B 11.D 12.A
二、填空题
13. 14. 15. 16.③④
三、解答题
17.解:(1)将得
(2)不等式即为
即
①当
②当
③.
18.解:
19.解:(1)设正面出现的次数为m,反面出现的次数为n,则,可得:
(2)
20.解法(一)
(1)证明:∵AE⊥平面AA1DD1,A1D⊥AD1,∴A1D⊥D1E
(2)设点E到面ACD1的距离为h,在△ACD1中,AC=CD1=,AD1=,
故
(3)过D作DH⊥CE于H,连D1H、DE,则D1H⊥CE,
∴∠DHD1为二面角D1―EC―D的平面角.
设AE=x,则BE=2-x
解法(二):以D为坐标原点,直线DA,DC,DD1分别为x,y,z轴,建立空间直角坐标系,设AE=x,则A1(1,0,1),D1(0,0,1),E(1,x,0),A(1,0,0)C(0,2,0)
(1)
(2)因为E为AB的中点,则E(1,1,0),从而,
,设平面ACD1的法向量为,则
也即,得,从而,所以点E到平面AD1C的距离为
(3)设平面D1EC的法向量,∴
由 令b=1, ∴c=2,a=2-x,
∴
依题意
∴(不合,舍去), .
∴AE=时,二面角D1―EC―D的大小为.
21.解:(1)方法一 用数学归纳法证明:
1°当n=1时,
∴,命题正确.
2°假设n=k时有
则
而
又
∴时命题正确.
由1°、2°知,对一切n∈N时有
方法二:用数学归纳法证明:
1°当n=1时,∴;
2°假设n=k时有成立,
令,在[0,2]上单调递增,所以由假设
有:即
也即当n=k+1时 成立,所以对一切
(2)下面来求数列的通项:所以
,
又bn=-1,所以
22.解:(1)设切点A、B坐标分别为,
∴切线AP的方程为:
切线BP的方程为:
解得P点的坐标为:
所以△APB的重心G的坐标为 ,
所以,由点P在直线l上运动,从而得到重心G的轨迹方程为:
(2)方法1:因为
由于P点在抛物线外,则
∴
同理有
∴∠AFP=∠PFB.
方法2:①当所以P点坐标为,则P点到直线AF的距离为:
即
所以P点到直线BF的距离为:
所以d1=d2,即得∠AFP=∠PFB.
②当时,直线AF的方程:
直线BF的方程:
所以P点到直线AF的距离为:
,同理可得到P点到直线BF的距离,因此由d1=d2,可得到∠AFP=∠PFB.
以下同个关于圆锥曲线的命题中
①设A、B为两个定点,k为非零常数,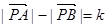 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②过定圆C上一定点A作圆的动弦AB,O为坐标原点,若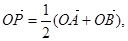 则动点P的轨迹为
则动点P的轨迹为
椭圆;
③方程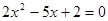 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线 有相同的焦点.
有相同的焦点.
其中真命题的序号为 (写出所有真命题的序号)
查看习题详情和答案>>
以下同个关于圆锥曲线的命题中
①设A、B为两个定点,k为非零常数,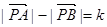 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②过定圆C上一定点A作圆的动点弦AB,O为坐标原点,若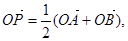 则动点P的轨迹为椭圆;
则动点P的轨迹为椭圆;
③方程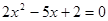 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线 有相同的焦点.
有相同的焦点.
其中真命题的序号为 (写出所有真命题的序号)
查看习题详情和答案>>
①设A、B为两个定点,k为非零常数,
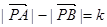 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;②过定圆C上一定点A作圆的动弦AB,O为坐标原点,若
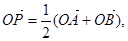 则动点P的轨迹为
则动点P的轨迹为椭圆;
③方程
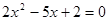 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;④双曲线
 有相同的焦点.
有相同的焦点.其中真命题的序号为 (写出所有真命题的序号)
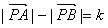 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线; 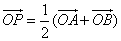 ,则动点P的轨迹为椭圆;
,则动点P的轨迹为椭圆; 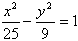 与椭圆
与椭圆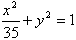 有相同的焦点。
有相同的焦点。