摘要:在.4.5.中同类根式有
网址:http://m.1010jiajiao.com/timu_id_194092[举报]
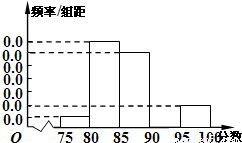
 某高校在2012年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
某高校在2012年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.(1)求出第4组的频率,并补全频率分布直方图;
(2)如果用分层抽样的方法从“优秀”和“良好”的学生中选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
(3)若该校决定在第4,5 组中随机抽取2名学生接受考官A的面试,第5组中有ξ名学生被考官A面试,求ξ的分布列和数学期望.
某高校在2012年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
(1)求出第4组的频率,并补全频率分布直方图;
(2)如果用分层抽样的方法从“优秀”和“良好”的学生中选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
(3)若该校决定在第4,5 组中随机抽取2名学生接受考官A的面试,第5组中有ξ名学生被考官A面试,求ξ的分布列和数学期望.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)求出第4组的频率,并补全频率分布直方图;
(2)如果用分层抽样的方法从“优秀”和“良好”的学生中选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
(3)若该校决定在第4,5 组中随机抽取2名学生接受考官A的面试,第5组中有ξ名学生被考官A面试,求ξ的分布列和数学期望.
 查看习题详情和答案>>
查看习题详情和答案>>
某高校在2012年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
(1)求出第4组的频率,并补全频率分布直方图;
(2)如果用分层抽样的方法从“优秀”和“良好”的学生中选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
(3)若该校决定在第4,5 组中随机抽取2名学生接受考官A的面试,第5组中有ξ名学生被考官A面试,求ξ的分布列和数学期望.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)求出第4组的频率,并补全频率分布直方图;
(2)如果用分层抽样的方法从“优秀”和“良好”的学生中选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
(3)若该校决定在第4,5 组中随机抽取2名学生接受考官A的面试,第5组中有ξ名学生被考官A面试,求ξ的分布列和数学期望.
 查看习题详情和答案>>
查看习题详情和答案>>
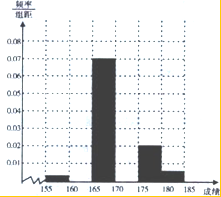 某校为了解高三学生的情况,现从期末文综考试成绩中随机抽取100名学生,按成绩分组,得到的频率分布表如图:
某校为了解高三学生的情况,现从期末文综考试成绩中随机抽取100名学生,按成绩分组,得到的频率分布表如图:| 组别 | 分组 | 频数 | 频率 |
| 1 | [155,160] | 2 | 0.020 |
| 2 | [155,160] | ① | 0.300 |
| 3 | [155,160] | 35 | 0.350 |
| 4 | [155,160] | 20 | 0.200 |
| 5 | [155,160] | 10 | ② |
| 6 | [155,160] | 3 | 0.030 |
| 合计 | 100 | 1.00 |
(2)若在第4、5组的30人中,用分层抽样抽取6名学生参加体育测试,请问:在第4、5组各抽取多少名学生参加测试?
(3)为了进一步获得研究资料,学校决定在第1组和第6组的学生中,随机抽取3名学生进行心理测试,求第1组中的A同学和第6组中的C同学被同时抽到的概率.
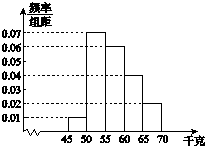 为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位:千克)全部介于45至70之间.将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70],得到如图所示的频率分布直方图.现采用分层抽样的方法,从第3,4,5组中随机抽取6名学生做初检.
为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位:千克)全部介于45至70之间.将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70],得到如图所示的频率分布直方图.现采用分层抽样的方法,从第3,4,5组中随机抽取6名学生做初检.