题目内容
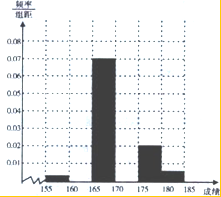 某校为了解高三学生的情况,现从期末文综考试成绩中随机抽取100名学生,按成绩分组,得到的频率分布表如图:
某校为了解高三学生的情况,现从期末文综考试成绩中随机抽取100名学生,按成绩分组,得到的频率分布表如图:| 组别 | 分组 | 频数 | 频率 |
| 1 | [155,160] | 2 | 0.020 |
| 2 | [155,160] | ① | 0.300 |
| 3 | [155,160] | 35 | 0.350 |
| 4 | [155,160] | 20 | 0.200 |
| 5 | [155,160] | 10 | ② |
| 6 | [155,160] | 3 | 0.030 |
| 合计 | 100 | 1.00 |
(2)若在第4、5组的30人中,用分层抽样抽取6名学生参加体育测试,请问:在第4、5组各抽取多少名学生参加测试?
(3)为了进一步获得研究资料,学校决定在第1组和第6组的学生中,随机抽取3名学生进行心理测试,求第1组中的A同学和第6组中的C同学被同时抽到的概率.
分析:(1)设表中①、②位置相应的数据分别为x、y,由频率、频数的关系可得
=0.3,y=
=0.1,解可得x、y的值,即可得答案;
(2)由图表可得,第4组有20人,第5组有10人,由分层抽样方法,计算可得答案;
(3)根据题意,第1组中有2人,设为A、B,第6组中有3人,设为C、D、E,列举从这5人中抽取3人的情况,分析可得其情况数目和A、C被同时抽到的情况数目,由等可能事件的概率公式,计算可得答案.
| x |
| 100 |
| 10 |
| 100 |
(2)由图表可得,第4组有20人,第5组有10人,由分层抽样方法,计算可得答案;
(3)根据题意,第1组中有2人,设为A、B,第6组中有3人,设为C、D、E,列举从这5人中抽取3人的情况,分析可得其情况数目和A、C被同时抽到的情况数目,由等可能事件的概率公式,计算可得答案.
解答: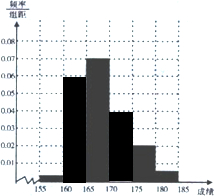 解:(1)设表中①、②位置相应的数据分别为x、y;
解:(1)设表中①、②位置相应的数据分别为x、y;
有
=0.3,则x=30,
y=
=0.1,
故表中①、②位置相应的数据分别为30、0.1;
补全频率分布直方图如图:
(2)由图表可得,第4组有20人,第5组有10人,共30人,
从中用分层抽样抽取6人,则第4组应抽取20×
=4人,
第5组应抽取10×
=2人,
故在第4组中应抽取4人,第5组应抽取2人;
(3)第1组中有2人,设为A、B,第6组中有3人,设为C、D、E,
从中抽取3人,其情况有(A,B,C)、(A,B,D)、(A,B,E)、(A,C,D)、(A,C,E)、
(A,D,E)、(B,C,D)、(B,C,E)、(B,D,E)、(C,D,E),共10种,
其中A、C同时被抽到的情况有(A,B,C)、(A,C,D)、(A,C,E),共3种,
则A、C同时被抽到的概率为
.
 解:(1)设表中①、②位置相应的数据分别为x、y;
解:(1)设表中①、②位置相应的数据分别为x、y;有
| x |
| 100 |
y=
| 10 |
| 100 |
故表中①、②位置相应的数据分别为30、0.1;
补全频率分布直方图如图:
(2)由图表可得,第4组有20人,第5组有10人,共30人,
从中用分层抽样抽取6人,则第4组应抽取20×
| 6 |
| 30 |
第5组应抽取10×
| 6 |
| 30 |
故在第4组中应抽取4人,第5组应抽取2人;
(3)第1组中有2人,设为A、B,第6组中有3人,设为C、D、E,
从中抽取3人,其情况有(A,B,C)、(A,B,D)、(A,B,E)、(A,C,D)、(A,C,E)、
(A,D,E)、(B,C,D)、(B,C,E)、(B,D,E)、(C,D,E),共10种,
其中A、C同时被抽到的情况有(A,B,C)、(A,C,D)、(A,C,E),共3种,
则A、C同时被抽到的概率为
| 3 |
| 10 |
点评:本题考查等可能事件的概率计算,涉及频率分步直方图与分层抽样方法的运用,注意认真分析题干频率分步表中的数据即可.

练习册系列答案
相关题目
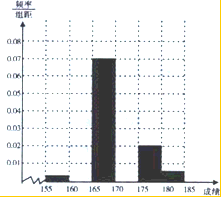 某校为了解高三学生的情况,现从期末文综考试成绩中随机抽取100名学生,按成绩分组,得到的频率分布表如图:
某校为了解高三学生的情况,现从期末文综考试成绩中随机抽取100名学生,按成绩分组,得到的频率分布表如图:
| 组别 | 分组 | 频数 | 频率 |
| 1 | [155,160] | 2 | 0.020 |
| 2 | [155,160] | ① | 0.300 |
| 3 | [155,160] | 35 | 0.350 |
| 4 | [155,160] | 20 | 0.200 |
| 5 | [155,160] | 10 | ② |
| 6 | [155,160] | 3 | 0.030 |
| 合计 | 100 | 1.00 |
(2)若在第4、5组的30人中,用分层抽样抽取6名学生参加体育测试,请问:在第4、5组各抽取多少名学生参加测试?
(3)为了进一步获得研究资料,学校决定在第1组和第6组的学生中,随机抽取3名学生进行心理测试,求第1组中的A同学和第6组中的C同学被同时抽到的概率.
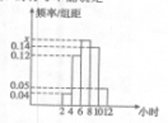
 (2011•开封一模)某校为了解高三学生在寒假期间的学习情况,抽查了100名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图),则这100名同学中学习时间在6到8小时内的人数为( )
(2011•开封一模)某校为了解高三学生在寒假期间的学习情况,抽查了100名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图),则这100名同学中学习时间在6到8小时内的人数为( )